Exercice : Devoir Trigonométrie 2024
Dans tous les exercices, on fera des dessins à l'aide de cercles trigonométriques
Exercice 1
.
Question
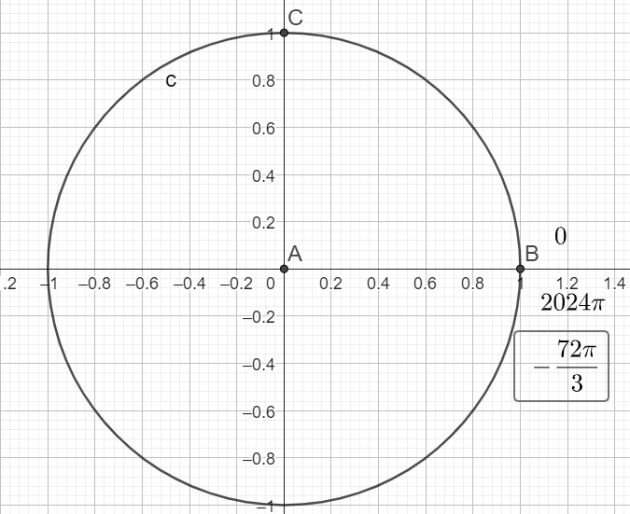
Donner la mesure principale des mesures \(\frac{-72\pi}{3}\) et \(2024\pi\)
Solution
\(\frac{\frac{-72\pi}{3}}{2\pi}=\frac{\frac{-72\pi}{3}}{\frac{2\pi}{1}}\)
\(\iff \frac{\frac{-72\pi}{3}}{2\pi}=\frac{-72\pi}{3} \times \frac{1}{2\pi}\)
\(\iff \frac{\frac{-72\pi}{3}}{2\pi}=\frac{-72\pi}{6\pi}\)
\(\iff \frac{\frac{-72\pi}{3}}{2\pi}=-12\)
donc \(\frac{-72\pi}{3}\) est égal à -12 tours.
\(\frac{-72\pi}{3} + 12 \times 2 \pi\)
\(=\frac{-72\pi}{3} +24 \pi\)
\(=\frac{-72\pi}{3} +\frac{72 \pi}{3}\)
\(=0 \in ]-\pi ;\pi]\)
La mesure principale de \(\frac{-72\pi}{3}\) est donc 0
\(\frac{2024\pi}{2\pi}=\frac{2024}{2}=1012\)
donc \(2024\pi\) est égal à 1012 tours.
\(2024 \pi - 1012 \times 2 \pi\)
\(=2024 \pi - 2024 \pi\)
\(=0 \in ]-\pi ;\pi]\)
La mesure principale de \(2024 \pi\) est donc 0
Exercice 2
Soit \(x \in [0 ;\frac{\pi}{2}]\), on sait que \(cos(x)=\frac{1+\sqrt{3}}{3}\)
Question
1. Dans quel intervalle de nombre doit se situer la valeur du cosinus.
Montrer que la valeur du cosinus donné dans l'énoncé respecte bien cette propriété.
Solution
Comme \(x \in [0 ;\frac{\pi}{2}]\), \(cos x \in [0 ;1]\)
or \(\frac{1+\sqrt{3}}{3} \simeq 0,91 \in [0 ;1]\)
donc la valeur de cosinus donnée dans l'énoncé correspond bien au cosinus d'un angle.
En déduire les valeurs exactes de :
Question
2. \(cos(-x)\) et \(cos( \pi -x)\)
Solution
\(cos(-x)= cos (x)\)
donc \(cos(-x)=\frac{1+\sqrt{3}}{3}\)
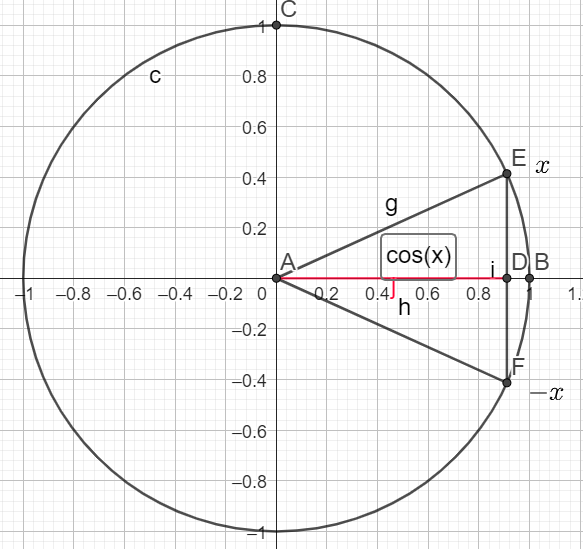
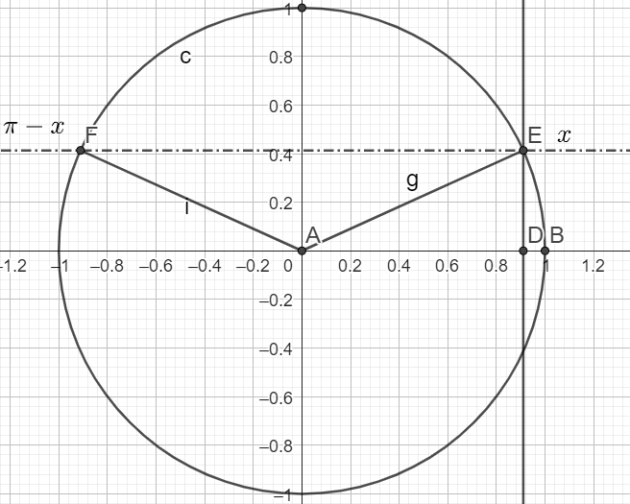
\(cos( \pi -x)=-cos(x)=-(\frac{1+\sqrt{2}}{3})\)
Question
3. \(sin(x)\) et \(sin(x - \frac{\pi}{2})\)
Solution
On utilise la relation trigonométrique :
\(cos^2(x)+sin^2(x)=1\)
\(\iff (\frac{1+\sqrt{3}}{3})^2+sin^2(x)=1\)
\(\iff \frac{1^2+2\sqrt{3}+\sqrt{3}^2}{9}+sin^2(x)=1\)
\(\iff \frac{1+2\sqrt{3}+3}{9}+sin^2(x)=1\)
\(\iff \frac{4+2\sqrt{3}}{9}+sin^2(x)=1\)
\(\iff sin^2(x)=1-(\frac{4+2\sqrt{3}}{9})\)
\(\iff sin^2(x)=\frac{9}{9}-(\frac{4+2\sqrt{3}}{9})\)
\(\iff sin^2(x)=\frac{5-2\sqrt{3}}{9}\)
\(\iff sin(x)=\frac{\sqrt{5-2\sqrt{3}}}{3}\) ou \(sin(x)=-\frac{\sqrt{5-2\sqrt{3}}}{3}\)
or \(x \in [0 ;\frac{\pi}{2}]\) donc \(sin x \ge 0\)
Finalement :
\(sin(x)=\frac{\sqrt{5-2\sqrt{3}}}{3}(\simeq 0,41)\)
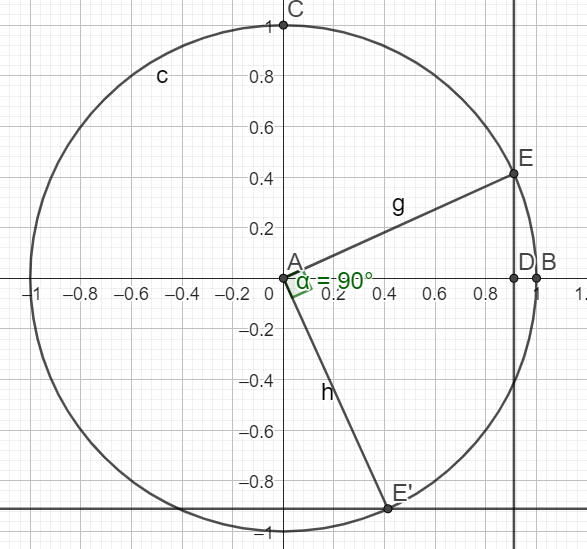
\(sin(x - \frac{\pi}{2})=-cos(x)=-(\frac{1+\sqrt{3}}{3})\)
Exercice 3
Expliquer brièvement mais soigneusement chacune des égalités.
Question
1. Sans utiliser la calculatrice , déterminer la valeur exacte de :
\(cos(\frac{\pi}{3})+cos(\frac{-5\pi}{6}) \times cos(\frac{-\pi}{3})\)
Solution
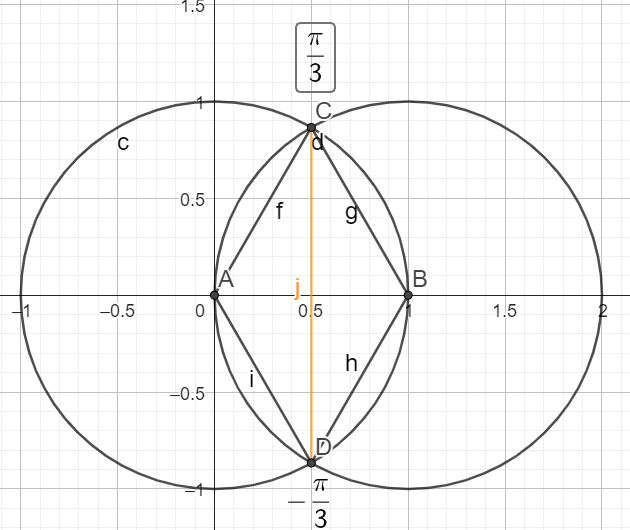
\(cos(\frac{\pi}{3})= \frac{1}{2}\)
\(cos(\frac{-\pi}{3})=cos(\frac{\pi}{3})= \frac{1}{2}\)
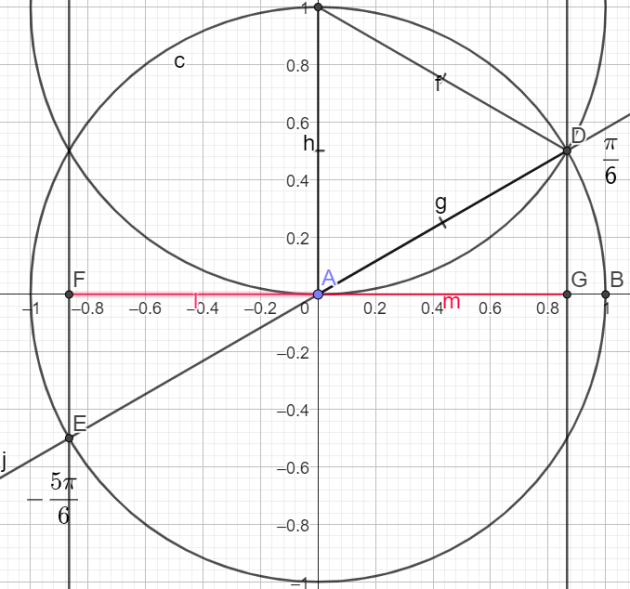
\(cos(\frac{-5\pi}{6})=cos(\frac{\pi}{6}-\pi)=-cos(\frac{\pi}{6})=-\frac{\sqrt{3}}{2}\)
\(cos(\frac{\pi}{3})+cos(\frac{-5\pi}{6}) \times cos(\frac{-\pi}{3})\)
\(=\frac{1}{2}+(-\frac{\sqrt{3}}{2}) \times \frac{1}{2}\)
\(=\frac{1}{2}-\frac{\sqrt{3}}{4}\)
\(=\frac{2}{4}-\frac{\sqrt{3}}{4}\)
\(=\frac{2-\sqrt{3}}{4}\)
Question
2.Ecrire le plus simplement possible :
\(cos(\frac{\pi}{8})-cos(\frac{7\pi}{8})+cos(\frac{10\pi}{16})+cos(\frac{6\pi}{16})\)
Solution
\(cos(\frac{\pi}{8})-cos(\frac{7\pi}{8})+cos(\frac{10\pi}{16})+cos(\frac{6\pi}{16})\)
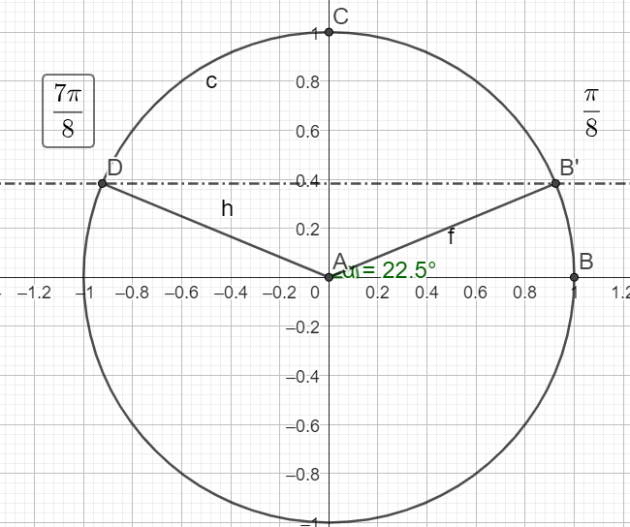
\(cos(\frac{7\pi}{8})=cos(\pi-\frac{\pi}{8})=-cos(\frac{\pi}{8})\)
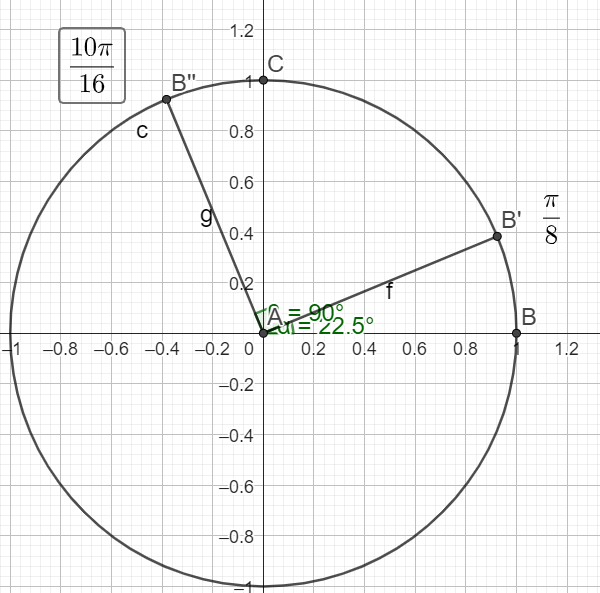
\(\frac{\pi}{2}+\frac{\pi}{8}=\frac{8\pi}{16}+\frac{2\pi}{16}=\frac{10\pi}{16}\)
donc \(cos(\frac{10\pi}{16})=cos(\frac{\pi}{2}+\frac{\pi}{8})=-sin(\frac{\pi}{8})\)
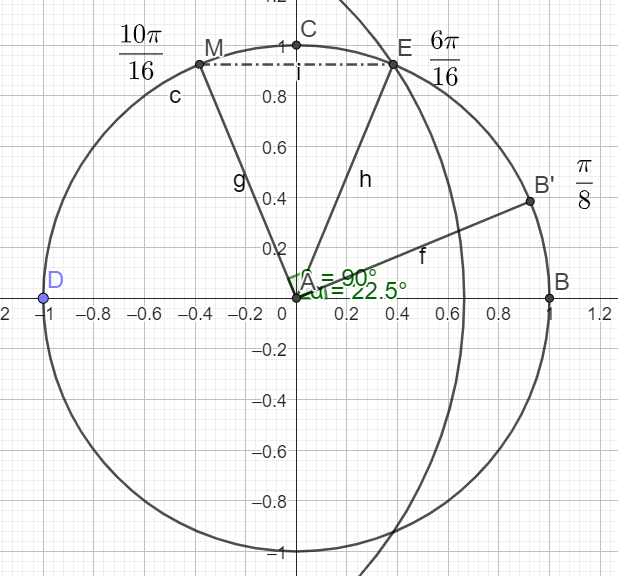
\(\pi-\frac{10\pi}{16}=\frac{16\pi}{16}-\frac{10\pi}{16}=\frac{6\pi}{16}\)
donc
\(cos(\frac{6\pi}{16})=cos(\pi-\frac{10\pi}{16})=-cos(\frac{10\pi}{16})=-(-sin(\frac{\pi}{8}))=sin(\frac{\pi}{8})\)
Finalement :
\(cos(\frac{\pi}{8})-cos(\frac{7\pi}{8})+cos(\frac{10\pi}{16})+cos(\frac{6\pi}{16})\)
\(=cos(\frac{\pi}{8})-(-cos(\frac{\pi}{8}))+sin(\frac{\pi}{8})+(-sin(\frac{\pi}{8}))\)
=\(2cos(\frac{\pi}{8})\)
Question
3.Ecrire le plus simplement possible :
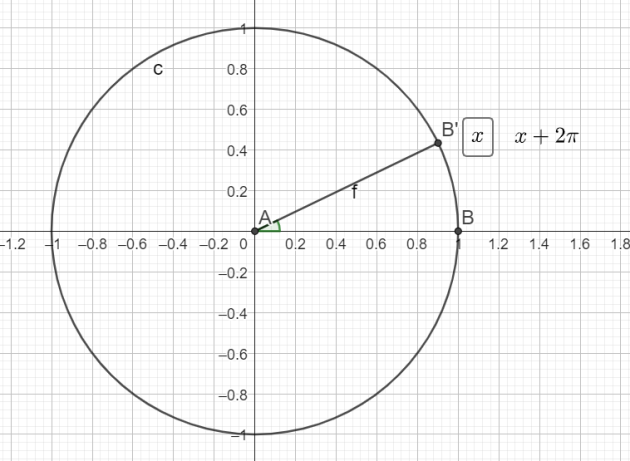
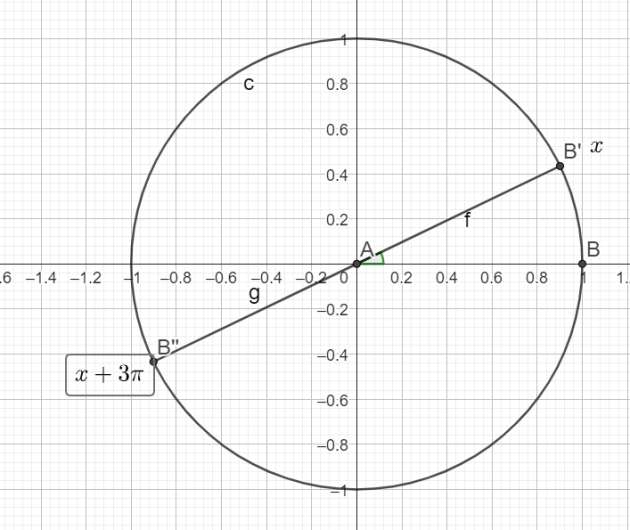
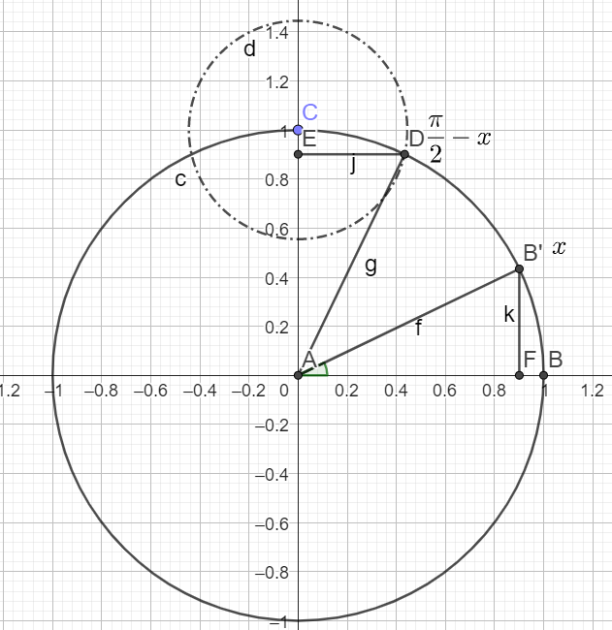
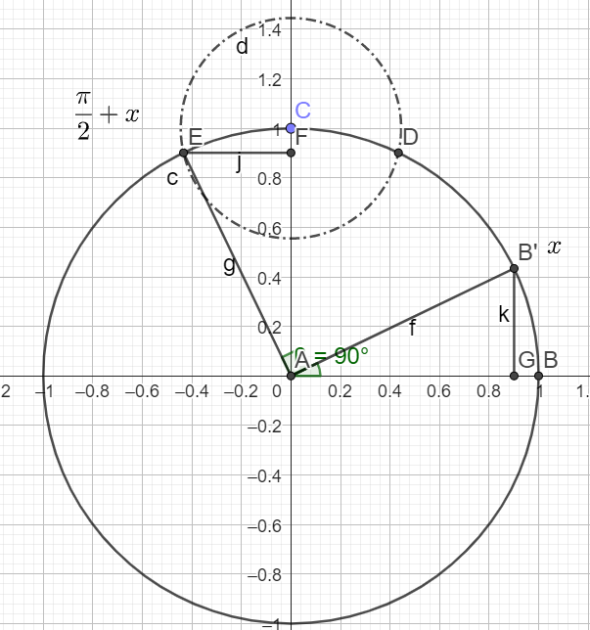
\(cos(x+2\pi)-sin(x+3\pi)+sin(\frac{\pi}{2}-x)+cos(\frac{\pi}{2}+x)\)
Question
4.Ecrire le plus simplement possible :
\(cos(2 \pi)+cos(\frac{\pi}{6})+sin(\frac{\pi}{6})+cos(\frac{\pi}{3})+sin(\frac{\pi}{3})+cos(\pi)\)
Solution
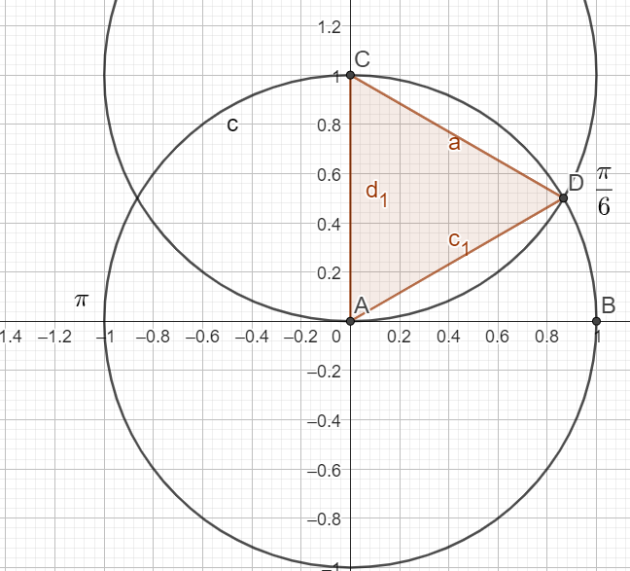
\(cos(\frac{\pi}{6})=\frac{\sqrt{3}}{2}\)
\(sin(\frac{\pi}{6})=\frac{1}{2}\)
\(cos(\pi)=-1\)
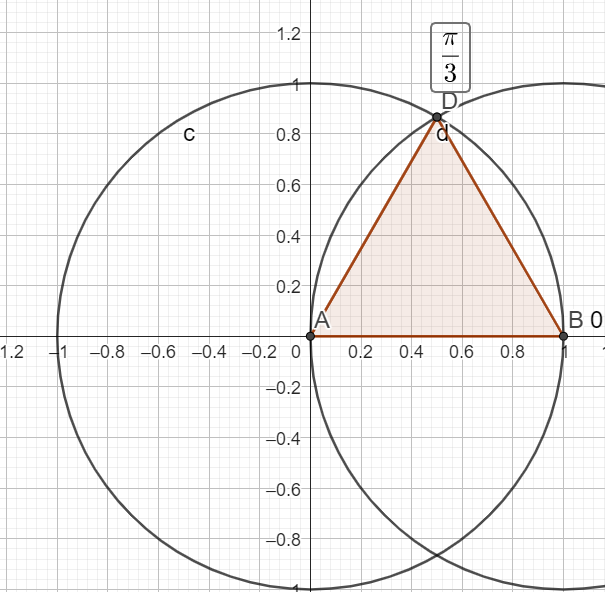
\(cos(2 \pi)=1\)
\(cos(\frac{\pi}{3})=\frac{1}{2}\)
\(sin(\frac{\pi}{3})=\frac{\sqrt{3}}{2}\)
\(cos(2 \pi)+cos(\frac{\pi}{6})+sin(\frac{\pi}{6})+cos(\frac{\pi}{3})+sin(\frac{\pi}{3})+cos(\pi)\)
\(=1+\frac{\sqrt{3}}{2}+\frac{1}{2}+\frac{1}{2}+\frac{\sqrt{3}}{2}-1\)
\(=1+\sqrt{3}\)
Exercice 4
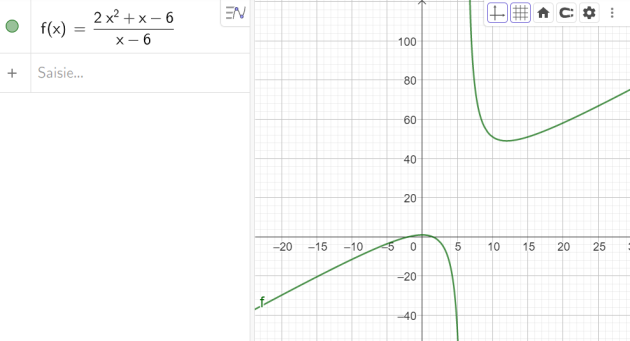
On définit la fonction \(f\) en posant :
\(f(x)=\frac{3x^2+x-6}{x-6}\)
Question
1.Spécifier l'ensemble de définition de la fonction \(f\)
Solution
Le dénominateur d'une fonction ne peut pas s'annuler donc on doit avoir :
\(x-6 \ne 0\)
\(\iff x \ne 6\)
donc \(D_f=\mathbb{R}\)\{6}
Question
2. Vérifier que pour tout nombre réel appartenant à l'intervalle \(]6 ;+\infty[\), on peut écrire \(f(x)\) sous la forme \(f(x)=3x+19+\frac{108}{x-6}\)
Solution
\(3x+19+\frac{108}{x-6}\)
\(=\frac{3x+19}{1}+\frac{108}{x-6}\)
\(=\frac{(3x+19)(x-6)}{x-6}+\frac{108}{x-6}\)
\(=\frac{(3x+19)(x-6)+108}{x-6}\)
\(=\frac{(3x^2-18x+19x-114)+108}{x-6}\)
\(=\frac{3x^2+x-6}{x-6}\)
On retrouve l'expression donnée dans l'énonce pour la fonction \(f\) donc :
\(f(x)=3x+19+\frac{108}{x-6}\)
Question
2.On note \(f'\) la dérivée de la fonction \(f\).
Donner l'expression de \(f'(x)\)
Solution
\(f(x)=\frac{3x^2+x-6}{x-6}=\frac{u}{v}\)
or \((\frac{u}{v})'=\frac{u'v-uv'}{v^2}\)
\(\begin{cases}u=3x^2+x-6\\v=x-6\end{cases}\)
\(\Rightarrow \begin{cases}u'=3 \times 2x+1\\v'=1\end{cases}\)
\(\Rightarrow \begin{cases}u'=6x+1\\v'=1\end{cases}\)
donc \(f'(x)=\frac{(6x+1)(x-6)-(3x^2+x-6)(1)}{(x-6)^2}\)
\(\iff f'(x)=\frac{(6x^2-36x+x-6)-(3x^2+x-6)}{(x-6)^2}\)
\(\iff f'(x)=\frac{6x^2-36x+x-6-3x^2-x+6}{(x-6)^2}\)
\(\iff f'(x)=\frac{3x^2-36x}{(x-6)^2}\)
Question
3. Etudier, sur l'intervalle \(]6 ;+\infty[\) le signe de \(f'(x)\)
Solution
\(f'(x)=\frac{3x^2-36x}{(x-6)^2}\)
Etude du signe du numérateur :
\(3x^2-36x=0\)
a=3 b=-36 c=0
\(\Delta=b^2-4ac\)
\(\iff \Delta=(-36)^2-4 \times 3 \times 0\)
\(\iff \Delta=1296\)
Comme le discriminant est positif,
l'équation \(3x^2-36x=0\) a deux solutions :
\(\begin{cases}x_1=\frac{-b-\sqrt{\Delta}}{2a}\\x_2=\frac{-b+\sqrt{\Delta}}{2a}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{-(-36)-\sqrt{1296}}{2 \times 3}\\x_2=\frac{-(-36)+\sqrt{1296}}{2 \times 3}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{36-36}{6}\\x_2=\frac{36+36}{6}\end{cases}\)
\(\iff \begin{cases}x_1=0\\x_2=\frac{72}{6}\end{cases}\)
\(\iff \begin{cases}x_1=0\\x_2=12\end{cases}\)
\(\color{magenta}{\text{Autre méthode pour trouver les solutions (plus courte):}}\)
\(3x^2-36x=0\)
\(\iff 3x(x-12)=0\)
\(\color{red}{\text{Propriété :}}\)
\(\color{red}{\text{Un produit de facteurs est nul}}\)
\(\color{red}{\text{si et seulement si }}\)
\(\color{red}{\text{un des facteurs au moins est égal à 0}}\)
\(\iff x=0\) ou \(x-12=0\)
\(\iff x=0\) ou \(x=12\)
Etude du signe du dénominateur :
\((x-6)^2=0 \iff x-6=0 \iff x=6\)
Le carré d'un nombre réel est toujours positif.
\(f(13)=\frac{2 \times 12^2+12-6}{12-6}\)
\(\iff f(12)=\frac{2 \times 144+6}{6}\)
\(\iff f(12)=\frac{288+6}{6}\)
\(\iff f(12)=\frac{294}{6}=49\)
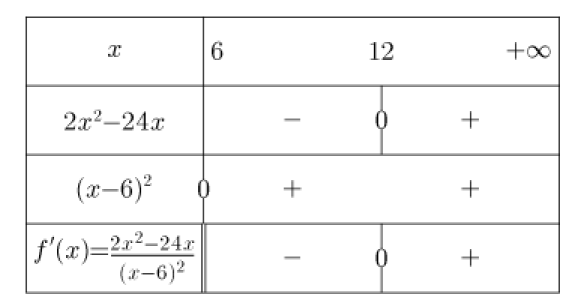
Question
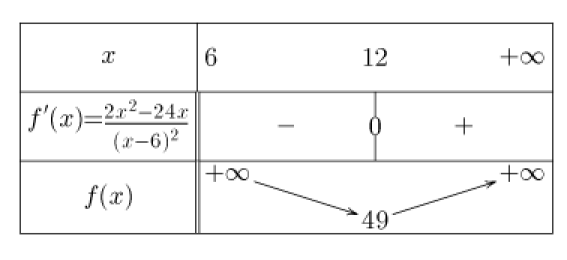
En déduire le tableau de variations de la fonction \(f\) sur l'intervalle \(]6 ;+\infty[\)
Question
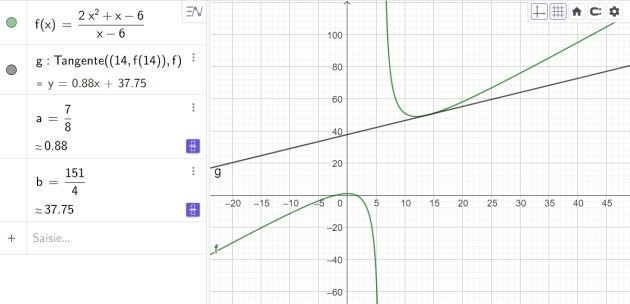
5.On note T la tangente à la courbe de la fonction \(f\) au point d'abscisse \(x\)=14.
Déterminer l'équation réduite de la droite T.
Solution
L'équation réduite de la tangente à la courbe de la fonction \(f\) au point d'abscisse \(x\)=\(a\) est :
\(y=f'(a)(x-a)+f(a)\)
donc
L'équation réduite de la tangente à la courbe de la fonction \(f\) au point d'abscisse \(x\)=\(14\) est :
\(y=f'(14)(x-14)+f(14)\)
\(f(14)=\frac{2 \times 14^2+14-6}{14-6}\)
\(\iff f(14)=\frac{2 \times 196+8}{8}\)
\(\iff f(14)=\frac{392+8}{8}\)
\(\iff f(14)=\frac{400}{8}=50\)
\(f'(14)=\frac{2 \times 14^2-24 \times 14}{(14-6)^2}\)
\(\iff f'(14)=\frac{2 \times 196-24 \times 14}{8^2}\)
\(\iff f'(14)=\frac{392-336}{8^2}\)
\(\iff f'(14)=\frac{56}{64}\)
\(\iff f'(14)=\frac{7}{8}\)
L'équation réduite de la tangente à la courbe de la fonction \(f\) au point d'abscisse \(x\)=\(14\) est donc:
\(y=f'(14)(x-14)+f(14)=\frac{7}{8}(x-14)+50\)
\(\iff y=\frac{7}{8}x-\frac{7}{8} \times 14+50\)
\(\iff y=\frac{7}{8}x-\frac{7}{4} \times 7+50\)
\(\iff y=\frac{7}{8}x-\frac{49}{4}+\frac{200}{4}\)
\(\iff y=\frac{7}{8}x+\frac{151}{4}\)