Exercice : Devoir Trigonométrie 2024-2
Exercice 1
.
Question
Sur le cercle trigonométrique \(\mathcal{C}\), placer le point M associé à la valeur \(\frac{\pi}{6}.\)
Solution
La mesure \(\frac{\pi}{6}\) correspond à un angle de \(\frac{180}{3}=60°\)
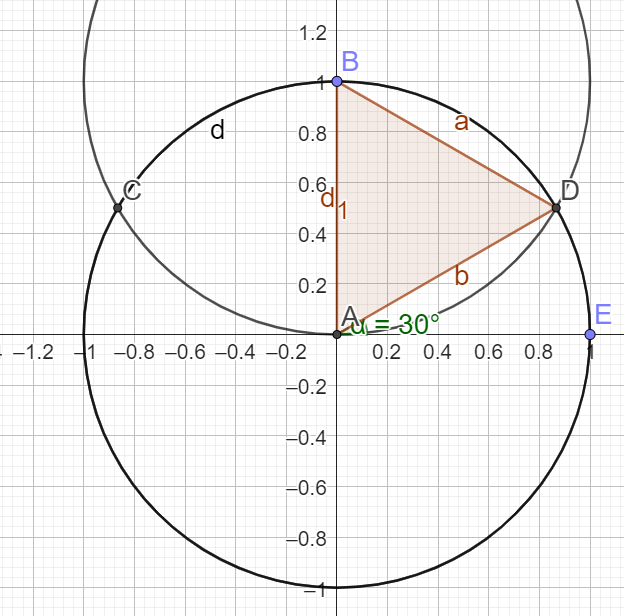
Question
2. Placer ensuite les points \(M_1\),\(M_2\) et \(M_3\) associés aux valeurs \(\frac{5\pi}{6},\frac{9\pi}{6}\) et \(-\frac{\pi}{6}\)
Solution
\(\frac{5\pi}{6}=\frac{6\pi}{6}-\frac{\pi}{6}=\pi-\frac{\pi}{6}\)
\(\frac{9\pi}{6}=\frac{3\pi}{2}\)
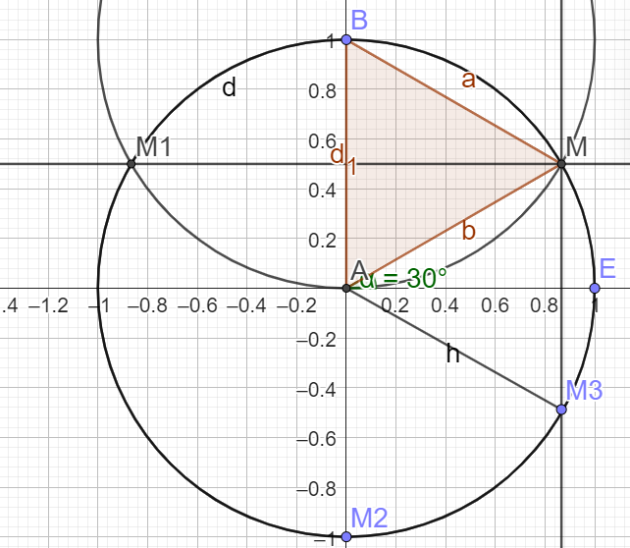
Question
3.Rappeler les valeurs de cosinus et de sinus \(\frac{\pi}{6}\)
Solution
\(\begin{cases}cos(\frac{\pi}{6})=\frac{\sqrt{3}}{2}\\sin(\frac{\pi}{6})=\frac{1}{2}\end{cases}\)
Question
4.En déduire les cosinus et sinus de \(\frac{5\pi}{6},\frac{9\pi}{6}\) et \(-\frac{\pi}{6}\)
Solution
\(\begin{cases}cos(\frac{5\pi}{6})=-\frac{\sqrt{3}}{2}\\sin(\frac{5\pi}{6})=\frac{1}{2}\end{cases}\)
\(\begin{cases}cos(\frac{9\pi}{6})=cos(\frac{3\pi}{2})=0\\sin(\frac{9\pi}{6})=sin(\frac{3\pi}{2})=-1\end{cases}\)
\(\begin{cases}cos(-\frac{\pi}{6})=\frac{\sqrt{3}}{2}\\sin(-\frac{\pi}{6})=-\frac{1}{2}\end{cases}\)
Exercice 2
Résoudre :
Question
- dans \(\mathbb{R}\) l'équation \(6cos(x)=-3\)
Solution
\(6cos(x)=-3\)
\(\iff cos(x)=-\frac{3}{6}=-\frac{1}{2}\)
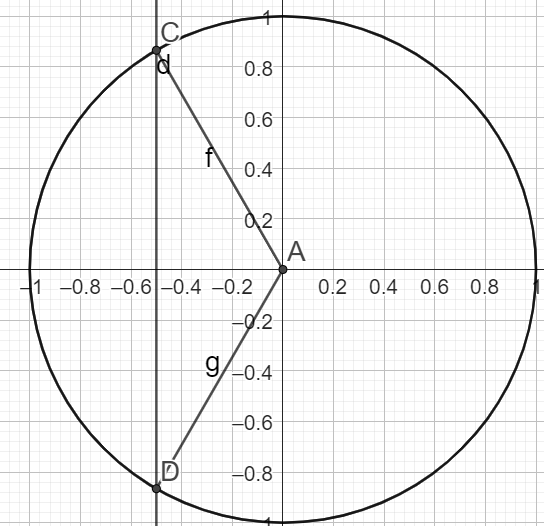
\(\Rightarrow S=\{\pi - \frac{\pi}{3}+2\pi \times k ; \pi+\frac{\pi}{3}+2\pi \times k \} k \in \mathbb{Z}\)
\(\iff S=\{\frac{3\pi}{3} - \frac{\pi}{3}+2\pi \times k ; \pi+\frac{\pi}{3}+2\pi \times k \} k \in \mathbb{Z}\)
\(\iff S=\{\frac{2\pi}{3}+2\pi \times k ; \frac{4\pi}{3}+2\pi \times k \} k \in \mathbb{Z}\)
Question
- dans \(]0 ;2 \pi]\)l'équation \(-\frac{\sqrt{3}}{2}+sin(x)=0\)
Solution
\(-\frac{\sqrt{3}}{2}+sin(x)=0\)
\(\iff sin(x)=\sqrt{3}{2}\)
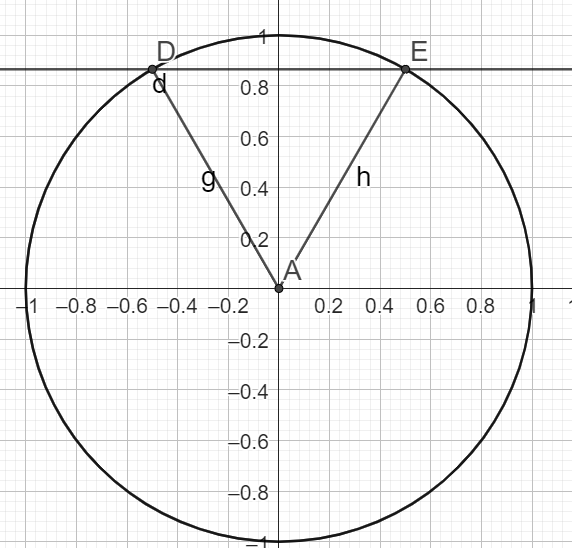
\(\Rightarrow S=\{\frac{\pi}{3} ;\pi - \frac{\pi}{3}\} k \in \mathbb{Z}\)
\(\iff S=\{\frac{\pi}{3} ; \frac{3\pi}{3}-\frac{\pi}{3}\} k \in \mathbb{Z}\)
\(\iff S=\{\frac{\pi}{3} ; \frac{2\pi}{3} \} k \in \mathbb{Z}\)
Question
- dans \([-\pi ;\pi[\) l'équation \(2sin(3x)=\sqrt{2}\)
Solution
\(2sin(3x)=\sqrt{2}\)
\(\iff sin(3x)=\frac{\sqrt{2}}{2}\)
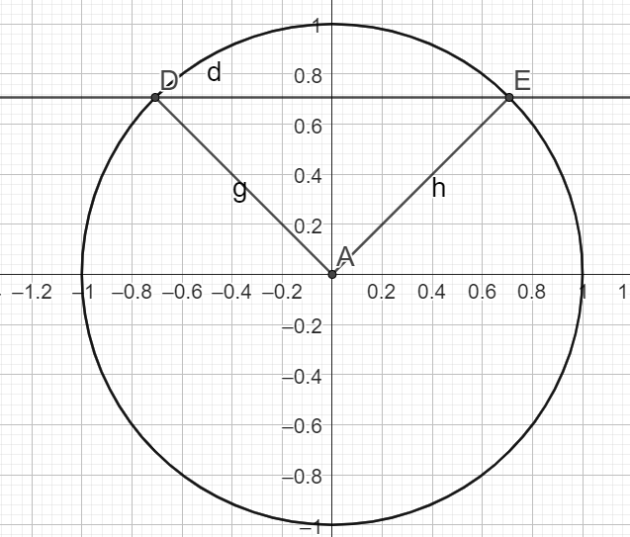
\(\Rightarrow 3x \in \{\frac{\pi}{4}+2\pi \times k ;\pi - \frac{\pi}{4} + 2\pi \times k \} k \in \mathbb{Z}\)
\(\iff 3x \in \{\frac{\pi}{4}+2\pi \times k ;\frac{4\pi}{4} - \frac{\pi}{4} + 2\pi \times k \} k \in \mathbb{Z}\)
\(\iff 3x \in \{\frac{\pi}{4}+2\pi \times k ;\frac{3\pi}{4} + 2\pi \times k \} k \in \mathbb{Z}\)
\(\iff x \in \{\frac{\pi}{12}+\frac{2\pi}{3} \times k ; \frac{\pi}{4}+\frac{2\pi}{3} \times k\} k \in \mathbb{Z}\)
Pour \(k=0\) : \(\frac{\pi}{12} ;\frac{\pi}{4}\)
Ces deux valeurs appartiennent à l'intervalle \([-\pi ;\pi[\). On les retient.
Pour \(k=1\) :
\(\frac{\pi}{12}+\frac{2\pi}{3} ;\frac{\pi}{4}+\frac{2\pi}{3}\)\(\)
\(\iff \frac{\pi}{12}+\frac{8\pi}{12} ;\frac{3\pi}{12}+\frac{8\pi}{12}\)\(\)
\(\iff \frac{9\pi}{12} ;\frac{11\pi}{12}\)
Ces deux valeurs appartiennent à l'intervalle \([-\pi ;\pi[\). On les retient.
Pour \(k=2\) :
\(\frac{\pi}{12}+\frac{2\pi}{3} \times 2;\frac{\pi}{4}+\frac{2\pi}{3}\) \times 2
\(\iff \frac{\pi}{12}+\frac{4\pi}{3} ;\frac{3\pi}{12}+\frac{4\pi}{3}\)
\(\iff \frac{\pi}{12}+\frac{16\pi}{12} ;\frac{3\pi}{12}+\frac{16\pi}{12}\)
\(\iff \frac{17\pi}{12} ;\frac{19\pi}{12}\)
Ces deux valeurs n'appartiennent à l'intervalle \([-\pi ;\pi[\).Elles sont trop grandes . On ne les retient pas . Inutile de prendre des valeurs de la variable \(k\) plus grandes.
Pour \(k=-1\) :
\(\frac{\pi}{12}-\frac{2\pi}{3} ;\frac{\pi}{4}-\frac{2\pi}{3}\)
\(\iff \frac{\pi}{12}-\frac{8\pi}{12} ;\frac{3\pi}{12}-\frac{8\pi}{12}\)
\(\iff \frac{-7\pi}{12} ;\frac{-5\pi}{12}\)
Ces deux valeurs appartiennent à l'intervalle \([-\pi ;\pi[\). On les retient.
Pour \(k=-2\) :
\(\frac{\pi}{12}-\frac{2\pi}{3} \times 2;\frac{\pi}{4}-\frac{2\pi}{3}\) \(\times 2\)
\(\iff \frac{\pi}{12}-\frac{4\pi}{3} ;\frac{3\pi}{12}-\frac{4\pi}{3}\)
\(\iff \frac{\pi}{12}-\frac{16\pi}{12} ;\frac{3\pi}{12}-\frac{16\pi}{12}\)
\(\iff \frac{-15\pi}{12} ;\frac{-13\pi}{12}\)
Ces deux valeurs n'appartiennent à l'intervalle \([-\pi ;\pi[\).Elles sont trop petites . On ne les retient pas . Inutile de prendre des valeurs de la variable \(k\) plus petites.
Finalement
\(S=\{\)\( \frac{-7\pi}{12} ;\frac{-5\pi}{12}\)\( \frac{\pi}{12} ;\frac{\pi}{4}\) ;\(\frac{9\pi}{12} ;\frac{11\pi}{12}\) \(\}\)
Exercice 3
On considère un réel \(x \in [-\frac{\pi}{2} ;\frac{\pi}{2}]\) tel que \(sin(x)=\frac{\sqrt{2}-\sqrt{6}}{4}\)
Question
Déterminer la valeur de \(cos(x)\)
Solution
On utilise la relation valable pour tout \(x \in \mathbb{R}\)
\(cos^2(x)+sin^2(x)=1\)
\(\iff cos^2(x)+\left ( \frac{\sqrt{2}-\sqrt{6}}{4} \right )^2 =1\)
\(\iff cos^2(x)+ \frac{(\sqrt{2}-\sqrt{6})^2}{16} =1\)
\(\iff cos^2(x)+ \frac{\sqrt{2}^2-2\sqrt{2} \times \sqrt{6} + \sqrt{6}^2}{16} =1\)
\(\iff cos^2(x)+ \frac{2-2\sqrt{12} + 6}{16} =1\)
\(\iff cos^2(x)+ \frac{8-2\sqrt{12} }{16} =1\)
\(\iff cos^2(x)+ \frac{8-2\sqrt{3 \times 4} }{16} =1\)
\(\iff cos^2(x)+ \frac{8-2 \times 2\sqrt{3} }{16} =1\)
\(\iff cos^2(x)+ \frac{8-4\sqrt{3} }{16} =1\)
\(\iff cos^2(x) =1- \frac{8-4\sqrt{3} }{16}\)
\(\iff cos^2(x) =\frac{16}{16}- \frac{8-4\sqrt{3} }{16}\)
\(\iff cos^2(x) =\frac{16-8+4\sqrt{3} }{16}\)
\(\iff cos^2(x) =\frac{8+4\sqrt{3} }{16}\)
On a remarqué que \(sin^2(x)=\frac{8-2\sqrt{3 \times 4} }{16}\)
\(\left ( \frac{\sqrt{2}+\sqrt{6}}{4} \right )^2=\frac{(\sqrt{2}+\sqrt{6})^2}{4^2}\)
On peut donc calculer :
\(\iff \left ( \frac{\sqrt{2}+\sqrt{6}}{4} \right )^2=\frac{\sqrt{2}^2+2\sqrt{2} \times \sqrt{6} +\sqrt{6}^2}{16}\)
\(\iff \left ( \frac{\sqrt{2}+\sqrt{6}}{4} \right )^2=\frac{2+2\sqrt{12} +6}{16}\)
\(\iff \left ( \frac{\sqrt{2}+\sqrt{6}}{4} \right )^2=\frac{8+2\sqrt{3 \times 4}}{16}\)
\(\iff \left ( \frac{\sqrt{2}+\sqrt{6}}{4} \right )^2=\frac{8+2 \times 2 \times \sqrt{3}}{16}\)
\(\iff \left ( \frac{\sqrt{2}+\sqrt{6}}{4} \right )^2=\frac{8+4\sqrt{3}}{16}\)
d'où \(cos(x)=\frac{\sqrt{2}+\sqrt{6}}{4}\) ou \(cos(x)=-\frac{\sqrt{2}+\sqrt{6}}{4}\)
Comme \(x \in [-\frac{\pi}{2} ;\frac{\pi}{2}]\), on sait que \(cos(x) \ge 0\)
finalement : \(\color{red}{cos(x)=\frac{\sqrt{2}+\sqrt{6}}{4}}\)
Question
2. On sait que \(x \in \{\frac{\pi}{12} ;\frac{5\pi}{12} ;\frac{-\pi}{12} ;\frac{-5\pi}{12}\}\)
Déterminer la valeur exacte de \(x\).
Solution
\(\begin{cases}sin(x)=\frac{\sqrt{2}-\sqrt{6}}{4}\\cos(x)=\frac{\sqrt{2}+\sqrt{6}}{4}\end{cases}\)
Comme \(sin(x)<0\) on en déduit que \(x \in \{\frac{-\pi}{12} ;\frac{-5\pi}{12}\}\)
Comme \(|cos(x)|>|sin(x)|\) on en déduit que \(x=\frac{-\pi}{12}\)
Exercice 4
On veut résoudre l'équation \(\sqrt{3}cos(x)=sin(x)\) dans \([0 ;2\pi[\)
Question
Démontrer que \(cos^2(x)=\frac{1}{4}\)
Solution
On utilise la relation valable pour tout \(x \in \mathbb{R}\)
\(cos^2(x)+sin^2(x)=1\)
\(\iff cos^2(x)+\left ( \sqrt{3}cos(x) \right )^2 =1\)
\(\iff cos^2(x)+\sqrt{3}^2 cos^2 (x)=1\)
\(\iff cos^2(x)+3 cos^2 (x)=1\)
\(\iff 4cos^2(x)=1\)
\(\iff cos^2(x)=\frac{1}{4}\)
Question
2. Résoudre l'équation \(cos^2(x)=\frac{1}{4}\) dans \([0 ;2\pi[\)
Solution
\(cos^2(x)=\frac{1}{4}\)
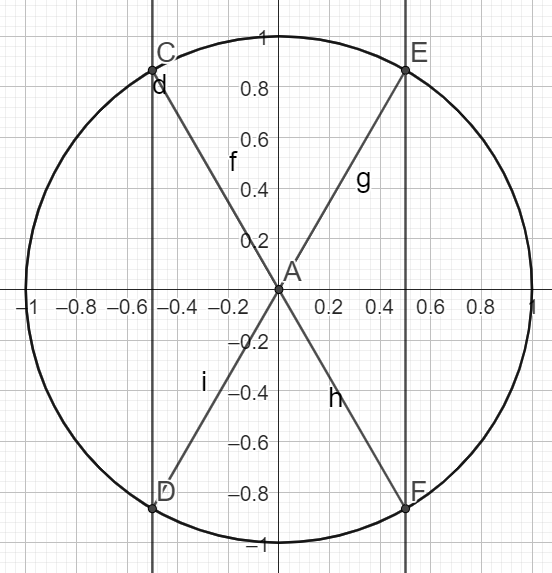
\(\iff cos(x)=\frac{1}{2}\) ou \(cos(x)=-\frac{1}{2}\)
\(\iff S=\{\frac{\pi}{3} ;\frac{2\pi}{3} ; \frac{4\pi}{3} ; \frac{5\pi}{3} \} \)
Question
3. Expliquer pourquoi \(cos(x)\) et \(sin(x)\) doivent avoir le même signe.
Solution
La relation donnée est :
\(\sqrt{3}cos(x)=sin(x)\)
Si \(cos(x) \ge 0\) alors \(\sqrt{3}cos(x)\ge0\) et donc \(sin(x)\ge0\)
Si \(cos(x)\le0\) alors \(\sqrt{3}cos(x)\le0\) et donc \(sin(x)\le0\)
Si \(sin(x)\ge0\) alors \(\frac{1}{\sqrt{3}}sin(x)\ge0\) et donc \(cos(x)\ge0\)
Si \(sin(x)\le0\) alors \(\frac{1}{\sqrt{3}}sin(x)\le0\) et donc \(cos(x)\le0\)
Donc \(cos(x)\) et \(sin(x)\) sont de même signe.
Question
4. En déduire les solutions de l'équation de départ.
Solution
D'après la question 2.
\(S=\{\frac{\pi}{3} ;\frac{2\pi}{3} ; \frac{4\pi}{3} ; \frac{5\pi}{3} \} \)
Or d'après la question 3., les expressions \(cos(x)\) et \(sin(x)\) sont de même signe
donc \(S=\{\frac{\pi}{3} ; \frac{4\pi}{3} \} \)