Exercice : Devoir Trigonométrie 2025 A
Sauf indication contraire, toute réponse devra être justifiée si ce n'est par une courte phrase.
Exercice 1
Question
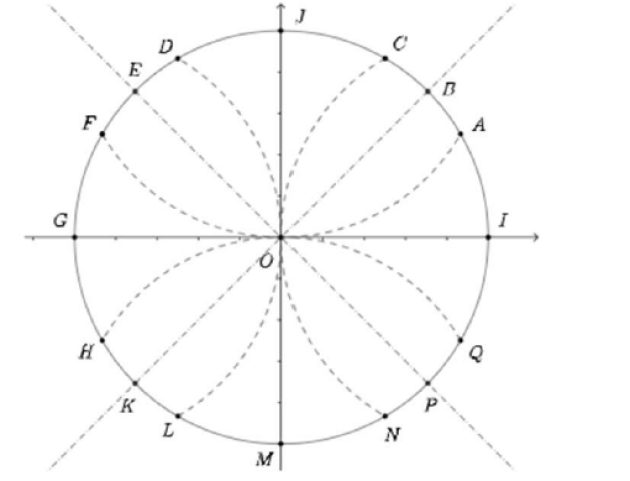
Compléter le tableau suivant sans justification :
\(x\) | \(\frac{\pi}{3}\) | \(\frac{5\pi}{6}\) | \(\frac{-17\pi}{3}\) | |||
|---|---|---|---|---|---|---|
Point correspondant | N | K | ||||
\(cos(x)\) | 0 | |||||
\(sin(x)\) | -1 |
Solution
\(x\) | \(\frac{\pi}{3}\) | \(-\frac{\pi}{3}\) | \(-\frac{3\pi}{4}\) | \(\frac{5\pi}{6}\) | \(\frac{-17\pi}{3}\) | \(\frac{-\pi}{2}\) ou \(\frac{3\pi}{2}\) |
|---|---|---|---|---|---|---|
Point correspondant | C | N | K | F | C | M |
\(cos(x)\) | \(\frac{1}{2}\) | \(\frac{1}{2}\) | \(-\frac{\sqrt{2}}{2}\) | \(-\frac{\sqrt{3}}{2}\) | \(\frac{1}{2}\) | 0 |
\(sin(x)\) | \(\frac{\sqrt{3}}{2}\) | \(-\frac{\sqrt{3}}{2}\) | \(-\frac{\sqrt{2}}{2}\) | \(\frac{1}{2}\) | \(\frac{\sqrt{3}}{2}\) | -1 |
Question
2. Compléter le tableau suivant sans justification :
Angle | \(\widehat{IOA}\) | \(\widehat{AOJ}\) | \(\widehat{IAO}\) |
|---|---|---|---|
Mesure en radians | |||
Mesure en degrés |
Solution
\(\widehat{AOJ}=\)\(\frac{\pi}{2}\)-\(\frac{\pi}{6}\)\(=\)\(\frac{3\pi}{6}\)-\(\frac{\pi}{6}\)=\(\frac{2\pi}{6}\)\(\)=\(\frac{\pi}{3}\)
La somme des mesures des angles d'un triangle vaut 180° soit \(\pi\) radians
Dans le triangle IAO isocèle en O :
\(\widehat{IAO}+\widehat{OIA}\)+\(\widehat{IOA}\)=\(\pi\)
or \(\widehat{IAO}=\widehat{OIA}\)
donc \(2\widehat{IAO}\)+\(\widehat{IOA}\)=\(\pi\)
\(\iff 2\widehat{IAO}\)+\(\frac{\pi}{6}\)=\(\pi\)
\(\iff 2\widehat{IAO}\)=\(\pi\)-\(\frac{\pi}{6}\)
\(\iff 2\widehat{IAO}\)=\(\frac{6\pi}{6}\)-\(\frac{\pi}{6}\)
\(\iff 2\widehat{IAO}\)=\(\frac{5\pi}{6}\)\(\)
\(\iff \widehat{IAO}\)=\(\frac{5\pi}{12}\)
Angle | \(\widehat{IOA}\) | \(\widehat{AOJ}\) | \(\widehat{IAO}\) |
|---|---|---|---|
Mesure en radians | \(\frac{\pi}{6}\) | \(\frac{\pi}{3}\) | \(\frac{5\pi}{12}\) |
Mesure en degrés | 30° | 60° | 75° |
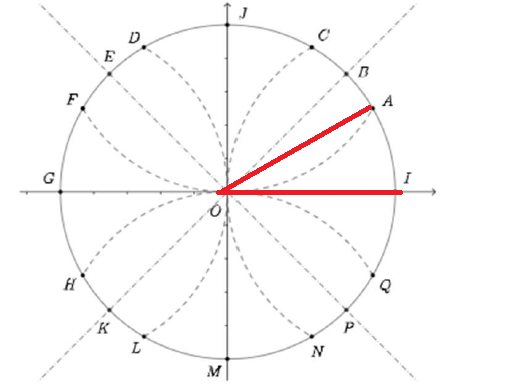
Question
3. Tracer le polygone régulier IACJDFGHLMNQ. Quel nom donne-t-on à ce polygone ?
Solution
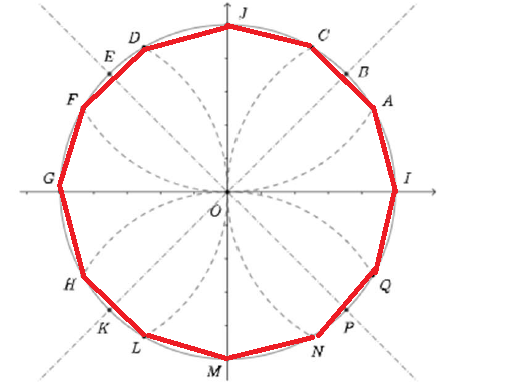
Le polygone régulier IACJDFGHLMNQ a douze côtés donc il s'agit d'un dodécagone régulier.
Question
4. Tracer la hauteur [AH'] issue du point A dans le triangle OAI.
D'après les valeurs remarquables de cosinus et sinus du cours, quelle est cette longueur ?
En déduire l'aire du triangle OAI puis du polygone régulier IACJDFGHLMNQ.
Solution
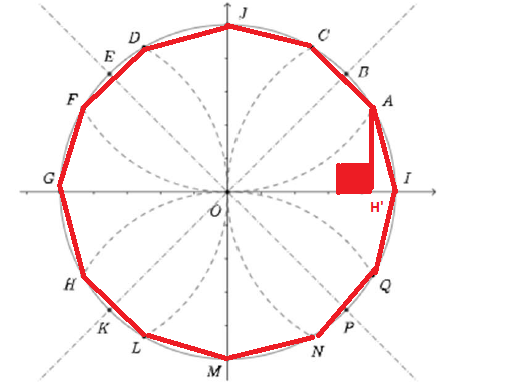
\(AH'=sin(x)\)
donc \(AH'=sin(\frac{\pi}{6})=\frac{1}{2}\)
Calcul de l'aire du triangle OAI :
\(A_{OAI}=\frac{Base \times Hauteur}{2}=\frac{OI \times AH'}{2}\)
\(\iff A_{OAI}=\frac{Base \times Hauteur}{2}=\frac{1 \times \sqrt{1}{2}}{2}=\frac{\sqrt{1}{2}}{\frac{2}{1}}=\frac{1}{2} \times \frac{1}{2}\)
\(\iff \iff A_{OAI}=\frac{1}{4}\)
L'aire du triangle OAI est donc \(\frac{1}{4}\)
Calcul de l'aire du du polygone régulier IACJDFGHLMNQ. :
\(A_{ IACJDFGHLMNQ}=12 \times A_{OAI}\)
\(\iff A_{ IACJDFGHLMNQ}=12 \times \frac{1}{4}=3\)
l'aire du du polygone régulier IACJDFGHLMNQ est donc 3
Question
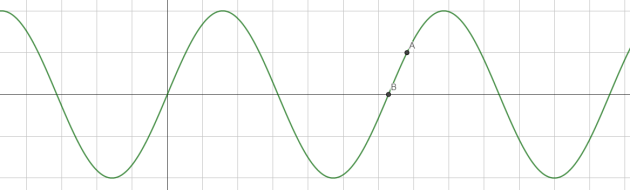
Graduer les axes.
Question
2. Donner les coordonnées des points A et B.
Solution
La fonction sinus est égale à \(\frac{1}{2}\) au point A.
Cette mesure correspond à la mesure principale \(\frac{\pi}{3}\)
donc le point A a pour coordonnées : \(A(\frac{\pi}{3}+2\pi ;\frac{1}{2})\)
soit \(A(\frac{\pi}{3}+\frac{6\pi}{3} ;\frac{1}{2})\)
\(\iff A(\frac{7\pi}{3} ;\frac{1}{2})\)
La fonction sinus est égale à \(0\) au point B.
Cette mesure correspond à la mesure principale \(0\)
donc le point B a pour coordonnées : \(B(0+2\pi ;0)\)
soit \(B(2\pi ;0)\)
Question
3. Jean annonce :
« Si on prolonge la courbe de la fonction sinus, le point symétrique du point A par rapport à l'origine du repère appartient à la courbe. »
Etes vous d'accord avec lui ? Quelle propriété de la fonction sinus cette propriété traduit-elle ?
Solution
La courbe de la fonction sinus est symétrique par rapport à l'origine du repère car la fonction sinus est \(\color{red}{impaire : f(-x)=-f(x)}\)
Le point symétrique du point A par rapport à l'origine du repère appartient donc à la courbe de la fonction sinus.
Question
4. Paul rajoute :
« Si on prolonge la courbe de la fonction sinus, le point symétrique du point A par rapport à l'axe des ordonnées appartient à la courbe. »
Etes vous d'accord avec lui ? Quelle propriété de la fonction sinus cette propriété traduirait-elle ?
Solution
La courbe de la fonction sinus n'est pas symétrique par rapport à l'axe des ordonnées car la fonction sinus \(\color{red}{\text{ n'est pas paire : } f(-x) \ne f(x)}\)
Le point symétrique du point A par rapport à l'axe des ordonnées n'appartient donc pas à la courbe de la fonction sinus.
Question
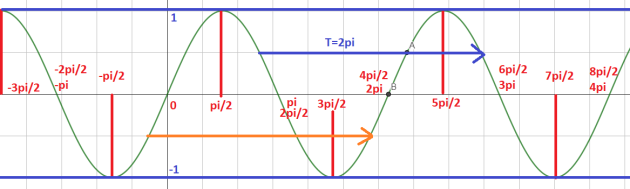
4.Tracer sur le graphique une période du signal précédent sous forme d'un vecteur de translation.
Donner la période de cette fonction.
Solution
La période de la fonction sinus est \(2\pi\).
La fonction sinus est \(2\pi\)-périodique.
Exercice 3
.
Question
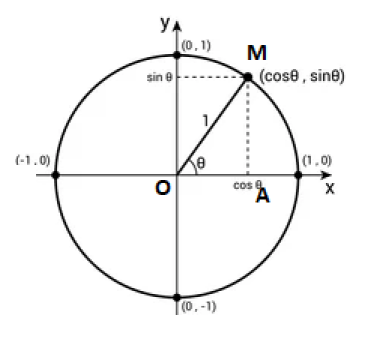
En utilisant les points portés sur le cercle trigonométrique ci-dessous et en utilisant le théorème de Pythagore, compléter après avoir redémontrer l'égalité suivante : \(cos^2(\theta)+sin^2(\theta)=\cdots\)
Solution
Le triangle OAM est rectangle en A, d'hypoténuse [OM],
d'après le théorème de Pythagore :
\(OM^2=OA^2+AM^2\)
\(\iff 1^2=(cos(\theta))^2+(sin(\theta))^2\)
car le cercle représenté ci-dessus est le cercle trigonométrique de rayon 1.
\(\iff cos^2(\theta)+sin^2(\theta)=1\)
Question
2. Sachant que \(\cos(\frac{\pi}{8})=\dfrac{\sqrt{2+\sqrt{2}}}{2}\), déterminer la valeur exacte de \(\cos(-\frac{\pi}{8})\)
Solution
\(\cos(-x)=cos(x)\)
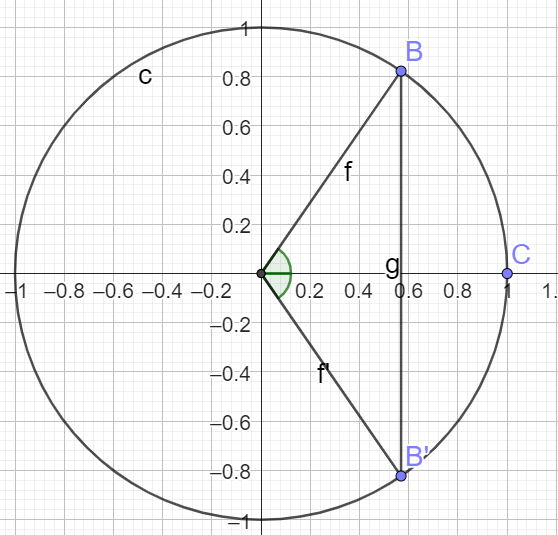
donc \(\cos(-\frac{\pi}{8})=\cos(\frac{\pi}{8})=\dfrac{\sqrt{2+\sqrt{2}}}{2}\)
Question
3. Donner la valeur de \((\cos(\frac{\pi}{8}))^2\) sous forme exacte, en déduire la valeur de \((\sin(\frac{\pi}{8}))^2\)
puis de \(\sin(\frac{\pi}{8}))\) et de \(\sin(-\frac{\pi}{8}))\)
Solution
\(\cos(\frac{\pi}{8})=\dfrac{\sqrt{2+\sqrt{2}}}{2}\)
\(\Rightarrow (\cos(\frac{\pi}{8}))^2=(\dfrac{\sqrt{2+\sqrt{2}}}{2})^2\)
\(\iff (\cos(\frac{\pi}{8}))^2=\dfrac{(\sqrt{2+\sqrt{2}})^2}{2^2}\)
\(\iff (\cos(\frac{\pi}{8}))^2=\dfrac{2+\sqrt{2}}{4}\)
\(\cos^2(\frac{\pi}{8})+sin^2(\frac{\pi}{8})=1\)
\(\iff sin^2(\frac{\pi}{8})=1-\cos^2(\frac{\pi}{8})\)
\(\iff sin^2(\frac{\pi}{8})=1-\dfrac{2+\sqrt{2}}{4}\)
\(\iff sin^2(\frac{\pi}{8})=\frac{4}{4}-\dfrac{2+\sqrt{2}}{4}\)
\(\iff sin^2(\frac{\pi}{8})=\frac{4-(2+\sqrt{2})}{4}\)
\(\iff sin^2(\frac{\pi}{8})=\frac{4-2-\sqrt{2}}{4}\)
\(\iff sin^2(\frac{\pi}{8})=\frac{2-\sqrt{2}}{4}\)
\(\iff sin(\frac{\pi}{8})=\frac{\sqrt{2-\sqrt{2}}}{2}\) ou \(\sin(\frac{\pi}{8})=-\frac{\sqrt{2-\sqrt{2}}}{2}\)
or \(\frac{\pi}{8} \in [-\frac{\pi}{2};-\frac{\pi}{2}]\) donc \(sin(\frac{\pi}{8})>0\)
Finalement \(\color{magenta}{sin(\frac{\pi}{8})=\frac{\sqrt{2-\sqrt{2}}}{2}}\)
\(\sin(-x)=-sin(x)\)

donc \(\color{magenta}{sin(-\frac{\pi}{8})=-sin(\frac{\pi}{8})=-\frac{\sqrt{2-\sqrt{2}}}{2}}\)
Exercice 4
Soit \(f\) la fonction définie sur l'ensemble des nombres réels \(\mathbb{R}\) par :
\(f(x)=sin(2x)+cos(x)sin(x)\)
Question
Calculer \(f(\frac{\pi}{4})\)
Solution
\(f(\frac{\pi}{4})=sin(2 \times \frac{\pi}{4})+cos(\frac{\pi}{4})sin(\frac{\pi}{4})\)
\(\iff f(\frac{\pi}{4})=sin( \frac{2\pi}{4})+cos(\frac{\pi}{4})sin(\frac{\pi}{4})\)
\(\iff f(\frac{\pi}{4})=sin( \frac{\pi}{2})+cos(\frac{\pi}{4})sin(\frac{\pi}{4})\)
\(sin( \frac{\pi}{2})=1\)
\(\begin{cases}cos(\frac{\pi}{4})=\frac{\sqrt{2}}{2}\\sin(\frac{\pi}{4})=\frac{\sqrt{2}}{2}\end{cases}\)
donc
\(f(\frac{\pi}{4})=1+\frac{\sqrt{2}}{2} \times \frac{\sqrt{2}}{2}\)
\(\iff f(\frac{\pi}{4})=1+\frac{\sqrt{2}^2}{2^2}\)
\(\iff f(\frac{\pi}{4})=1+\frac{2}{4}\)
\(\iff f(\frac{\pi}{4})=1+\frac{1}{2}\)
\(\iff f(\frac{\pi}{4})=\frac{2}{2}+\frac{1}{2}\)
\(\iff \color{magenta}{f(\frac{\pi}{4})=\frac{3}{2}}\)
Question
2. Calculer \(f(\frac{\pi}{6})\)
Solution
\(f(\frac{\pi}{6})=sin(2 \times \frac{\pi}{6})+cos(\frac{\pi}{6})sin(\frac{\pi}{6})\)
\(\iff f(\frac{\pi}{6})=sin( \frac{2\pi}{6})+cos(\frac{\pi}{6})sin(\frac{\pi}{6})\)
\(\iff f(\frac{\pi}{6})=sin( \frac{\pi}{3})+cos(\frac{\pi}{6})sin(\frac{\pi}{6})\)
\(sin( \frac{\pi}{3})=\frac{\sqrt{3}}{2}\)
\(\begin{cases}cos(\frac{\pi}{6})=\frac{\sqrt{3}}{2}\\sin(\frac{\pi}{6})=\frac{1}{2}\end{cases}\)
donc
\(f(\frac{\pi}{6})=\frac{\sqrt{3}}{2}+ \frac{\sqrt{3}}{2} \times \frac{1}{2}\)
\(\iff f(\frac{\pi}{6})=\frac{\sqrt{3}}{2}+ \frac{\sqrt{3}}{4}\)
\(\iff f(\frac{\pi}{6})=\frac{2\sqrt{3}}{4}+ \frac{\sqrt{3}}{4}\)
\(\iff \color{magenta}{f(\frac{\pi}{6})=\frac{3\sqrt{3}}{4}}\)
On rappelle qu'une fonction est \(\pi\) périodique
si et seulement si pour tout \(x\in \mathbb{R}\) \(f(x+\pi)=f(x)\)
Question
3. Démontrer que la fonction \(f\) est \(\pi\) périodique.
Solution
\(f(x+\pi)=sin(2(x+\pi))+cos(x+\pi)sin(x+\pi)\)
\(\iff f(x+\pi)=sin(2x+2\pi)+cos(x+\pi)sin(x+\pi)\)
\(f(x+\pi)=sin(2x+2\pi)+cos(x+\pi)sin(x+\pi)\)
la fonction sinus est \(2\pi\)-périodique donc \(sin(2x+2\pi)=sin(2x)\)
\(\begin{cases}cos(x+\pi)=-cos(x)\sin(x+\pi)=-sin(x)\end{cases}\)
\(\Rightarrow f(x+\pi)=sin(2x)+(-cos(x))(-sin(x))\)
\(\iff f(x+\pi)=sin(2x)+cos(x)sin(x)=f(x)\)
La fonction \(f\) est donc \(\pi\) périodique.
Question
4. Déduire des questions précédentes les valeurs de \(f(\frac{13\pi}{6})\) et de \(f(\frac{-5\pi}{6})\)
Solution
\(f(\frac{13\pi}{6})=f(\frac{\pi}{6}+\frac{12\pi}{6})=f(\frac{\pi}{6}+2\pi)=f(\frac{\pi}{6}+\pi+\pi)=f(\frac{\pi}{6}+\pi)=f(\frac{\pi}{6})\)
car la fonction \(f\) est \(\pi\) périodique.
Finalement \(f(\frac{13\pi}{6})=f(\frac{\pi}{6})=\frac{3\sqrt{3}}{4}\)
\(f(\frac{\pi}{6})=f(\frac{-5\pi}{6}+\pi)=f(\frac{-5\pi}{6})\)
car la fonction \(f\) est \(\pi\) périodique.
Finalement \(f(\frac{-5\pi}{6})=f(\frac{\pi}{6})=\frac{3\sqrt{3}}{4}\)
On rappelle qu'une fonction est paire
si et seulement si pour tout \(x\in \mathbb{R}\) \(f(-x)=f(x)\)
On rappelle qu'une fonction est impaire
si et seulement si pour tout \(x\in \mathbb{R}\) \(f(-x)=-f(x)\)
Question
5. La fonction \(f\) est-elle paire ? La fonction \(f\) est-elle impaire ?
Solution
\(f(-x)=sin(2(-x))+cos(-x)sin(-x)\)
\(sin(2(-x))=-sin(2x)\)
\(\begin{cases}cos(-x)=cos(x)\\sin(-x)=-sin(x)\end{cases}\)
\(f(-x)=-sin(2x)-cos(x)sin(x)\)
donc \(f(-x)=-f(x)\)
donc la fonction \(f\) est \(\color{magenta}{impaire.}\)