Exercice : DM Trigonométrie 2023
Exercice 1
Déterminer la mesure principale des angles suivants :
Question
Angle en radians | 17\(\pi\) | \(\frac{15\pi}{4}\) | \(\frac{27\pi}{3}\) | \(\frac{49\pi}{2}\) | \(\frac{-67\pi}{6}\) | \(\frac{2345\pi}{11}\) | \(\frac{4879\pi}{13}\) | \(2356\pi\) | \(54\pi\) |
|---|---|---|---|---|---|---|---|---|---|
Mesure principale |
Solution
\(\frac{17\pi}{2\pi}=\frac{17}{2}=8,5\)
\(17\pi- 8 \times 2\pi=17\pi-16\pi=\pi \in ]-\pi ;\pi]\)
La mesure principale de \(17\pi\) est donc \(\pi\)
\(\frac{\frac{15\pi}{4}}{2\pi}=\frac{\frac{15\pi}{4}}{\frac{2\pi}{1}}=\frac{15\pi}{4} \times \frac{1}{2\pi}=\frac{15\pi}{8\pi}=\frac{15}{8}\)
\(\frac{8}{8}<\frac{15}{8}<\frac{16}{8}\)
\(\iff 1<\frac{15}{8}<2\)
\(\frac{15\pi}{4}- 1 \times 2\pi=\frac{15\pi}{4}-\frac{2\pi}{1}=\frac{15\pi}{4}-\frac{8\pi}{4}=\frac{7\pi}{4} \notin ]-\pi ;\pi]\)
\(\frac{15\pi}{4}- 2 \times 2\pi=\frac{15\pi}{4}-\frac{4\pi}{1}=\frac{15\pi}{4}-\frac{16\pi}{4}=\frac{-\pi}{4} \in ]-\pi ;\pi]=]-\frac{4\pi}{4} ;\frac{4\pi}{4}]\)
La mesure principale de \(\frac{15\pi}{4}\) est donc \(\frac{-\pi}{4}\)
\(\frac{27\pi}{3}=9\pi=8\pi +\pi = 4 \times 2\pi +\pi\)
La mesure principale de \(\frac{27\pi}{3}\) est donc \(\pi\)
\(\frac{\frac{49\pi}{2}}{2\pi}=\frac{\frac{49\pi}{2}}{\frac{2\pi}{1}}=\frac{49\pi}{2} \times \frac{1}{2\pi}=\frac{49\pi}{4\pi}=\frac{49}{4}\)
\(\frac{48}{4}<\frac{49}{4}<\frac{52}{4}\)
\(\iff 12<\frac{49}{4}<13\)
\(\frac{49\pi}{2}- 12 \times 2\pi=\frac{49\pi}{2}-\frac{24\pi}{1}=\frac{49\pi}{2}-\frac{48\pi}{2}=\frac{\pi}{2} \in ]-\pi ;\pi]\)
La mesure principale de \(\frac{49\pi}{2}\) est donc \(\frac{\pi}{2}\)
\(\frac{-67\pi}{6}\)
\(\frac{\frac{-67\pi}{6}}{2\pi}=\frac{\frac{-67\pi}{6}}{\frac{2\pi}{1}}=\frac{-67\pi}{6} \times \frac{1}{2\pi}=\frac{-67\pi}{12\pi}=\frac{-67}{12}\)
\(\frac{-72}{12}<\frac{-67}{12}<\frac{-60}{15}\)
\(\iff -6<\frac{-67}{12}<-7\)
\(\frac{-67\pi}{6}+ 6 \times 2\pi=\frac{-67\pi}{6}+\frac{12\pi}{1}=\frac{-67\pi}{6}+\frac{72\pi}{6}=\frac{5\pi}{6} \in ]-\pi ;\pi]\)
La mesure principale de \(\frac{-67\pi}{6}\) est donc \(\frac{5\pi}{6}\)
\(\frac{2345\pi}{11}\)
\(\frac{\frac{2345\pi}{11}}{2\pi}=\frac{\frac{2345\pi}{11}}{\frac{2\pi}{1}}=\frac{2345\pi}{11} \times \frac{1}{2\pi}=\frac{2345\pi}{22\pi}=\frac{2345}{22}\)
\(\frac{2332}{22}<\frac{2345}{22}<\frac{2354}{22}\)
\(\iff 106<\frac{2345}{22}<107\)
\(\frac{2345\pi}{11}-106 \times 2\pi=\frac{2345\pi}{11}-212\pi\)
\(\iff \frac{2345\pi}{11}-106 \times 2\pi=\frac{2345\pi}{11}-\frac{2332\pi}{11}=\frac{13\pi}{11} \notin ]-\pi ;\pi]=]-\frac{11\pi}{11} ;\frac{11\pi}{11}]\)
\(\frac{2345\pi}{11}-107 \times 2\pi=\frac{2345\pi}{11}-214\pi\)
\(\iff \frac{2345\pi}{11}-107 \times 2\pi=\frac{2345\pi}{11}-\frac{2354\pi}{11}=\frac{-9\pi}{11} \notin ]-\pi ;\pi]=]-\frac{11\pi}{11} ;\frac{11\pi}{11}]\)
La mesure principale de \(\frac{2345\pi}{11}\) est donc \(\frac{-9\pi}{11}\)
\(\frac{4879\pi}{13}\)
\(\frac{\frac{4879\pi}{13}}{2\pi}=\frac{\frac{4879\pi}{13}}{\frac{2\pi}{1}}=\frac{4879\pi}{13} \times \frac{1}{2\pi}=\frac{4879}{26}\)
\(\frac{4862}{26}<\frac{4879}{26}<\frac{4888}{26}\)
\(\iff 187<\frac{4879}{26}<188\)
\(\frac{4879\pi}{13}-187 \times 2\pi=\frac{4879\pi}{13}-374\pi\)
\(\iff \frac{4879\pi}{13}-187 \times 2\pi=\frac{4879\pi}{13}-\frac{4862\pi}{13}=\frac{17\pi}{13} \notin ]-\pi ;\pi]=]-\frac{13\pi}{13} ;\frac{13\pi}{13}]\)
\(\frac{4879\pi}{13}-188 \times 2\pi=\frac{4879\pi}{13}-376\pi\)
\(\iff \frac{4879\pi}{13}-188 \times 2\pi=\frac{4879\pi}{13}-\frac{4888\pi}{13}=\frac{-9\pi}{13} \in ]-\pi ;\pi]=]-\frac{13\pi}{13} ;\frac{13\pi}{13}]\)
La mesure principale de \(\frac{4879\pi}{13}\) est donc \(\frac{-9\pi}{13}\)
\(2356\pi= 1178 \times 2\pi+0\)
La mesure principale de \(2356\pi\) est donc 0
\(54\pi=27 \times 2\pi +0\)
La mesure principale de \(54\pi\) est donc 0
Angle en radians | 17\(\pi\) | \(\frac{15\pi}{4}\) | \(\frac{27\pi}{3}\) | \(\frac{49\pi}{2}\) | \(\frac{-67\pi}{6}\) | \(\frac{2345\pi}{11}\) | \(\frac{4879\pi}{13}\) | \(2356\pi\) | \(c\) |
|---|---|---|---|---|---|---|---|---|---|
Mesure principale | \(\pi\) | \(\frac{-\pi}{4}\) | \(\pi\) | \(\frac{\pi}{2}\) | \(\frac{5\pi}{6}\) | \(\frac{-9\pi}{11}\) | \(\frac{-9\pi}{13}\) | 0 | 0 |
Exercice 2 :
Déterminer la valeur des nombres suivants :
Question
\(a = cos\left ( \frac{5\pi}{4} \right)\)
Question
\(b= cos\left ( -\frac{4\pi}{3} \right)\)
Question
\(c= sin\left ( \frac{25\pi}{6} \right)\)
Solution
\(c= sin\left ( \frac{25\pi}{6} \right)\)
\(\frac{\frac{25\pi}{6} }{2\pi}=\frac{\frac{25\pi}{6} }{\frac{2\pi}{1}}=\frac{25\pi}{6} \times \frac{1}{2\pi}=\frac{25}{12}\)
\(\frac{24}{12}<\frac{25}{12}<\frac{36}{12}\)
\(\iff 2<\frac{25}{12}<3\)
\(\frac{25\pi}{6} -2 \times 2\pi=\frac{25\pi}{6} -4\pi\)
\(\iff \frac{25\pi}{6} -2 \times 2\pi=\frac{25\pi}{6} -\frac{24\pi}{6}=\frac{\pi}{6} \in ]-\pi ;\pi]=]-\frac{6\pi}{6} ;\frac{6\pi}{6}]\)
donc \(c= sin\left ( \frac{25\pi}{6} \right)= sin\left ( \frac{\pi}{6} \right)=\frac{1}{2}\)
Question
\(d= sin\left ( -\frac{235\pi}{2} \right)\)
Solution
\(d= sin\left ( -\frac{235\pi}{2} \right)\)
\(\frac{-\frac{235\pi}{2} }{2\pi}=\frac{-\frac{235\pi}{2} }{\frac{2\pi}{1}}=-\frac{235\pi}{2} \times \frac{1}{2\pi}=-\frac{235}{4}\)
\(\frac{-240}{4}<-\frac{235}{4}<\frac{-236}{4}\)
\(\iff -60<\frac{25}{12}<-59\)
\(-\frac{235\pi}{2}+60 \times 2\pi=-\frac{235\pi}{2} +120\pi\)
\(\iff -\frac{235\pi}{2}+60 \times 2\pi=-\frac{235\pi}{2}+\frac{240\pi}{2}=\frac{5\pi}{2} \notin ]-\pi ;\pi]=]-\frac{2\pi}{2} ;\frac{2\pi}{2}]\)
\(-\frac{235\pi}{2}+59 \times 2\pi=-\frac{235\pi}{2} +118\pi\)
\(\iff -\frac{235\pi}{2}+59 \times 2\pi=-\frac{235\pi}{2}+\frac{236\pi}{2}=\frac{\pi}{2} \in ]-\pi ;\pi]=]-\frac{2\pi}{2} ;\frac{2\pi}{2}]\)
donc \(d= sin\left ( -\frac{235\pi}{2} \right)=sin\left (\frac{\pi}{2} \right)=0\)
Question
\(e= tan \left ( \frac{57\pi}{3} \right)\)
Solution
\(e= tan \left ( \frac{57\pi}{3} \right)=tan \left ( 19\pi \right)=tan \left ( \pi +9 \times 2\pi \right)\)
\(\iff e= tan \left ( \pi \right)=\frac{sin\left ( \pi \right)}{cos \left ( \pi \right)}\)
\(\iff e= tan \left ( \pi \right)=\frac{0}{-1}=0\)
Question
\(f= tan \left (-478\pi \right)\)
Solution
\(f= tan \left (-478\pi \right)=\frac{sin\left ( -239 \times 2\pi \right)}{cos \left ( -239 \times 2\pi \right)}\)
\(\iff f=\frac{0}{1}=0\)
Exercice 3 :
On donne \(sin\left ( \frac{7\pi}{10} \right)=\frac{1 +\sqrt{5}}{4}\)
Question
1. Donner la valeur exacte de \(cos\left ( \frac{7\pi}{10} \right)\)
Solution
\(cos^2\left ( \frac{7\pi}{10} \right)+sin^2\left ( \frac{7\pi}{10} \right)=1\)
\(\iff cos^2\left ( \frac{7\pi}{10} \right)+\left ( \frac{1 +\sqrt{5}}{4} \right)^2 =1\)
\(\iff cos^2\left ( \frac{7\pi}{10} \right)+ \frac{(1 +\sqrt{5})^2}{4^2} =1\)
\(\iff cos^2\left ( \frac{7\pi}{10} \right)+\frac{1 +2\sqrt{5}+5}{16} =1\)
\(\iff cos^2\left ( \frac{7\pi}{10} \right)+\frac{6 +2\sqrt{5}}{16} =1\)
\(\iff cos^2\left ( \frac{7\pi}{10} \right)=1-\frac{6 +2\sqrt{5}}{16}\)
\(\iff cos^2\left ( \frac{7\pi}{10} \right)=\frac{16}{16}-\frac{6 +2\sqrt{5}}{16}\)
\(\iff cos^2\left ( \frac{7\pi}{10} \right)=\frac{16-6-2\sqrt{5}}{16}\)
\(\iff cos^2\left ( \frac{7\pi}{10} \right)=\frac{10-2\sqrt{5}}{16}\)
\(\iff cos\left ( \frac{7\pi}{10} \right)=\sqrt{\frac{10-2\sqrt{5}}{16}} ou cos\left ( \frac{7\pi}{10} \right)=-\sqrt{\frac{10-2\sqrt{5}}{16}}\)
\(\iff cos\left ( \frac{7\pi}{10} \right)=\frac{\sqrt{10-2\sqrt{5}}}{\sqrt{16}} ou cos\left ( \frac{7\pi}{10} \right)=-\frac{\sqrt{10-2\sqrt{5}}}{\sqrt{16}}\)
\(\iff cos\left ( \frac{7\pi}{10} \right)=\frac{\sqrt{10-2\sqrt{5}}}{4} ou cos\left ( \frac{7\pi}{10} \right)=-\frac{\sqrt{10-2\sqrt{5}}}{4}\)
or \(\frac{7\pi}{10} \in [\frac{\pi}{2} ;\pi]=[\frac{5\pi}{10} ;\frac{10\pi}{10}]\)
donc \(cos\left ( \frac{7\pi}{10} \right)<0\)
et finalement \(cos\left ( \frac{7\pi}{10} \right)=-\frac{\sqrt{10-2\sqrt{5}}}{4}\)
Question
2. En déduire la valeur exacte de \(cos\left ( \frac{\pi}{5} \right)\)
Question
et \(sin\left ( \frac{17\pi}{10} \right)\)
Solution
\(sin\left ( \frac{17\pi}{10} \right)=sin\left ( \frac{10\pi}{10} +\frac{7\pi}{10} \right)\)
\(\iff sin\left ( \frac{17\pi}{10} \right)=sin\left (\pi +\frac{7\pi}{10} \right)\)
or \(sin\left ( x+ \pi \right )=-sin\left (x \right)\)
\(\iff sin\left ( \frac{17\pi}{10} \right)=-sin\left (\frac{7\pi}{10} \right)\)
\(\iff sin\left ( \frac{17\pi}{10} \right)=-\frac{1 +\sqrt{5}}{4}\)
Exercice 4
On donne \(cos(\frac{\pi}{16})=\frac{1}{2}\sqrt{2+\sqrt{2+\sqrt{2}}}\)
Question
1. Démontrer que \(sin(\frac{\pi}{16})=\frac{1}{2} \sqrt{2-\sqrt{2+\sqrt{2}}}\)
Solution
\(cos^2(x)+sin^2(x)=1\)
\(cos^2(\frac{\pi}{16})+sin^2(\frac{\pi}{16})=1\)
or \(cos(\frac{\pi}{16})=\frac{1}{2}\sqrt{2+\sqrt{2+\sqrt{2}}}\)
\(\iff cos^2(\frac{\pi}{16})+sin^2(\frac{\pi}{16})=1\)
\(\iff (\frac{1}{2}\sqrt{2+\sqrt{2+\sqrt{2}}})^2+sin^2(\frac{\pi}{16})=1\)
\(\iff \frac{1}{4}(2+\sqrt{2+\sqrt{2}})+sin^2(\frac{\pi}{16})=1\)
\(\iff sin^2(\frac{\pi}{16})=1-\frac{1}{4}(2+\sqrt{2+\sqrt{2}})\)
\(\iff sin^2(\frac{\pi}{16})=\frac{4}{4}-\frac{1}{4}(2+\sqrt{2+\sqrt{2}})\)
\(\iff sin^2(\frac{\pi}{16})=\frac{4-(2+\sqrt{2+\sqrt{2}})}{4}\)
\(\iff sin^2(\frac{\pi}{16})=\frac{4-2-\sqrt{2+\sqrt{2}}}{4}\)
\(\iff sin^2(\frac{\pi}{16})=\frac{2-\sqrt{2+\sqrt{2}}}{4}\)
\(\iff sin^2(\frac{\pi}{16})=\frac{1}{4}(2-\sqrt{2+\sqrt{2}})\)
\(\iff sin(\frac{\pi}{16})=\frac{1}{2}(\sqrt{2-\sqrt{2+\sqrt{2}}}\)
ou
\(sin(\frac{\pi}{16})=-\frac{1}{2}(\sqrt{2-\sqrt{2+\sqrt{2}}})\)
\(\frac{\pi}{16} \in [0 ;\frac{\pi}{2}]=[0 ;\frac{8\pi}{16}]\)
donc \(sin(\frac{\pi}{16})>0\)
d'où finalement
\(sin(\frac{\pi}{16})=\frac{1}{2}(\sqrt{2-\sqrt{2+\sqrt{2}}})\)
Question
2. En déduire la valeur exacte de \(cos(\frac{-7\pi}{16})\)
Solution
\(cos(\frac{-7\pi}{16})=cos(\frac{-8\pi}{16}+\frac{\pi}{16})\)
\(\iff cos(\frac{-7\pi}{16})=cos(\frac{-\pi}{2}+\frac{\pi}{16})\)
\(\iff cos(\frac{-7\pi}{16})=cos(\frac{-\pi}{2}+\frac{\pi}{16})\)
\(\iff cos(\frac{-7\pi}{16})=sin(\frac{\pi}{16})\)
\(\iff cos(\frac{-7\pi}{16})=\frac{1}{2}(\sqrt{2-\sqrt{2+\sqrt{2}}}\)
Question
et \(sin(\frac{17\pi}{16})\)
Solution
\(sin(\frac{17\pi}{16})=sin(\frac{16\pi}{16}+\frac{\pi}{16})\)
\(\iff sin(\frac{17\pi}{16})=sin(\pi+\frac{\pi}{16})\)
\(sin(\pi + x) =-sin(x)\)
donc \(sin(\frac{17\pi}{16})=-sin(\frac{\pi}{16})\)
\(\iff sin(\frac{17\pi}{16})=-\frac{1}{2}(\sqrt{2-\sqrt{2+\sqrt{2}}}\)
Exercice 5
Simplifier les expressions suivantes :
Question
1. A = \(sin(\pi + x) + cos(\frac{\pi}{2}-x)+ cos(\frac{\pi}{2}+x)+ sin(\pi-x)\)
Solution
\(sin(\pi + x) =-sin(x)\)

\(cos(\frac{\pi}{2}-x)=sin(x)\)
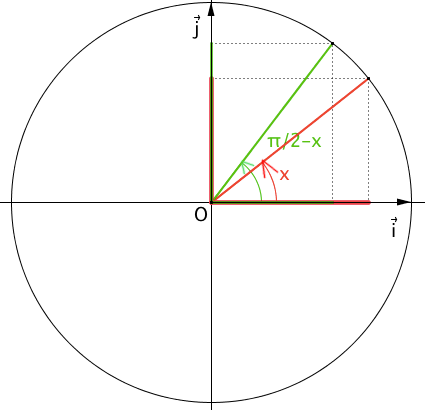
\(cos(\frac{\pi}{2}+x)=-sin(x)\)
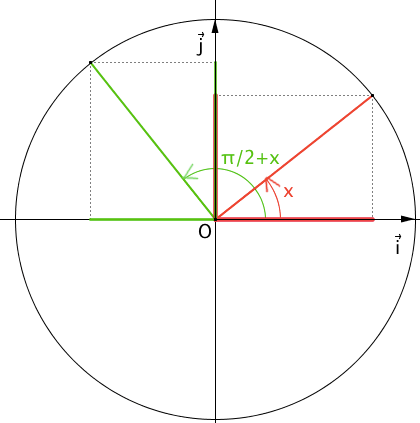
\(sin(\pi-x)=sin(x)\)
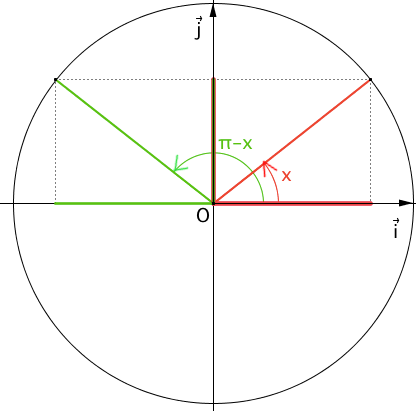
A = \(sin(\pi + x) + cos(\frac{\pi}{2}-x)+ cos(\frac{\pi}{2}+x)+ sin(\pi-x)\)
\(\iff A =- sin(x) + sin(x)-sin(x)+ sin(x)\)
\(\iff A =0\)
Question
2. B = \(cos(x) + cos( \frac{\pi}{2}+ x)+ cos(x+\frac{3 \pi}{2})+ cos(\pi + x)\)
Solution
\(cos(\frac{\pi}{2}+x)=-sin(x)\)

\(cos(x+\frac{3 \pi}{2})=sin(x)\)
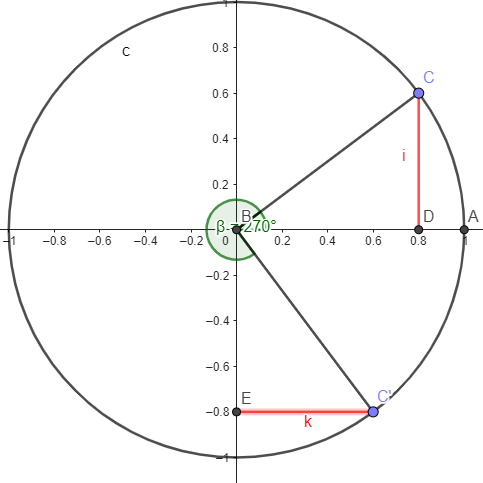
\(cos(\pi + x)=-cos(x)\)

B = \(cos(x) + cos( \frac{\pi}{2}+ x)+ cos(x+\frac{3 \pi}{2})+ cos(\pi + x)\)
\(\iff B = cos(x) -sin(x)+ sin(x)- cos(x)\)
\(\iff B =0\)
Question
3. C = \(sin(x-\frac{\pi}{2})+ cos (x + \pi) + cos(x-\frac{\pi}{2})+ sin(\pi-x)\)
Solution
\(sin(x-\frac{\pi}{2})=-cos(x)\)
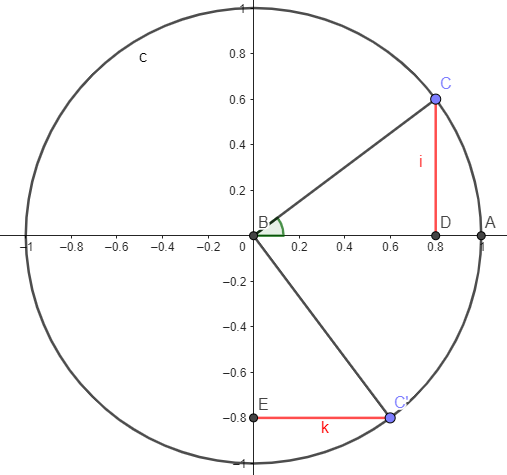
\(cos (x + \pi)=-cos(x)\)

\(cos(x-\frac{\pi}{2})=sin(x)\)

\(sin(\pi-x)=sin(x)\)

C = \(sin(x-\frac{\pi}{2})+ cos (x + \pi) + cos(x-\frac{\pi}{2})+ sin(\pi-x)\)
\(\iff C = -cos(x)-cos (x) + sin(x)+ sin(x)\)
\(\iff C = 2sin(x)-2cos(x)\)
\(\iff C = 2(sin(x)-cos(x))\)
Question
4. \(D = sin^2 x + 2 cos^2 x- 1\)
Solution
\(cos²(x)+sin^2(x)=1\)
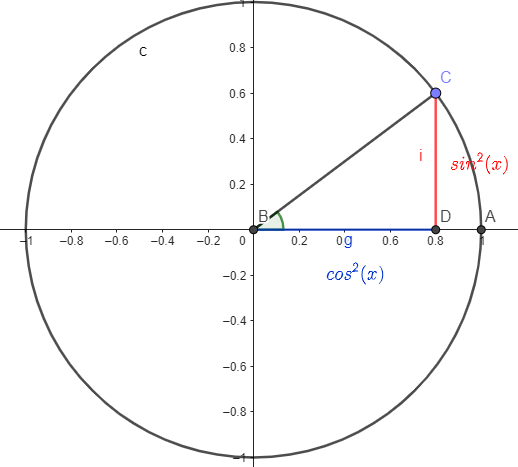
\(D = sin^2 x + cos^2 x + cos^2 x - 1\)
\(\iff D = 1 + cos^2 x - 1\)
\(\iff D = cos^2 x\)
Question
5.\( E = sin^2 x - cos^2 x\)
Solution

\(cos²(x)+sin^2(x)=1\)
\(\iff cos²(x)=1-sin^2(x)\)
ou
\(sin^2(x)=1-cos²(x)\)
\(E = sin^2 x - cos^2 x\)
\(\iff E = (1-cos²(x)) - cos^2 x\)
\(\iff E = 1-cos²(x) - cos^2 x\)
\(\iff E = 1-2cos²(x)\)
ou
\(\iff E = sin^2 x - (1-sin^2(x))\)
\(\iff E = sin^2 x - 1+sin^2(x)\)
\(\iff E = 2sin^2 x - 1\)
Question
\(6. F = (cos x + sin x)^2 + (cos x -sin x)^2\)
Solution
\(F = (cos x + sin x)^2 + (cos x -sin x)^2\)
\(\iff F = cos^2 x + 2cos(x)sin (x)+sin^2 x + cos^2 x -2cos(x)sin x+sin^2 x\)
\(\iff F = cos^2 x +sin^2 x + cos^2 x +sin^2 x\)

\(cos²(x)+sin^2(x)=1\)
\(\iff F =1+1=2\)
Exercice 6
On définit une fonction f sur l'intervalle ]-1;+\(\infty\)[ en posant, pour tout nombre réel \(x\) appartenant à cet intervalle :
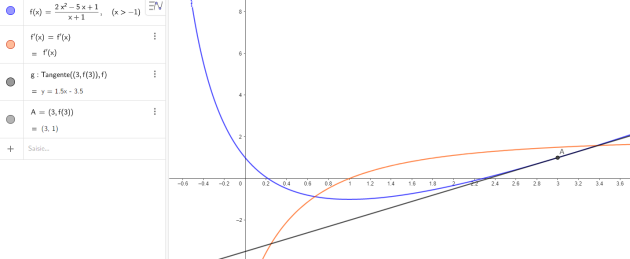
\(f (x) =\frac{2x^2 - 5x + 1}{x + 1}\)
Question
1. Vérifier que, pour tout nombre réel \(x\) appartenant à l'intervalle ]-1;+\(\infty\)[, on peut écrire \(f(x)\) sous la forme \(f(x) = 2x - 7 +\frac{8}{x + 1}\)
Solution
\(f (x) =\frac{2x^2 - 5x + 1}{x + 1}\) :
Valeur interdite :
\(x+1=0\)
\(\iff x \ne -1\)
donc \(D_f=\mathbb{R}\\{-1} \cap ]-1 ;+\infty[=]-1 ;+\infty[\)
\(2x - 7 +\frac{8}{x + 1}=\frac{2x - 7}{1} +\frac{8}{x + 1}\)
\(\iff 2x - 7 +\frac{8}{x + 1}=\frac{(2x - 7)(x + 1)}{1(x + 1)} +\frac{8}{x + 1}\)
\(\iff 2x - 7 +\frac{8}{x + 1}=\frac{(2x - 7)(x + 1)}{x + 1} +\frac{8}{x + 1}\)
\(\iff 2x - 7 +\frac{8}{x + 1}=\frac{2x \times x +2 x \times 1- 7 \times x -7 \times 1}{x + 1} +\frac{8}{x + 1}\)
\(\iff 2x - 7 +\frac{8}{x + 1}=\frac{2x^2 +2 x- 7x -7}{x + 1} +\frac{8}{x + 1}\)
\(\iff 2x - 7 +\frac{8}{x + 1}=\frac{2x^2 -5x -7}{x + 1} +\frac{8}{x + 1}\)
\(\iff 2x - 7 +\frac{8}{x + 1}=\frac{2x^2 -5x -7+8}{x + 1}\)
\(\iff 2x - 7 +\frac{8}{x + 1}=\frac{2x^2 -5x +1}{x + 1}\)
On retrouve l'expression de la fonction \(f\)
donc \(f(x)=2x - 7 +\frac{8}{x + 1}\) pour tout \(x \in ]-1 ;+\infty[\)
Question
2. On note \(f'\) la dérivée de la fonction \(f\). Calculer \(f'(x)\).
Solution
\(f (x) =\frac{2x^2 - 5x + 1}{x + 1}=\frac{u}{v}\)
or \((\frac{u}{v})'=(\frac{u'v-uv'}{v^2})\)
\(\begin{cases}u=2x^2 - 5x + 1\\v=x+1\end{cases}\)
\(\rightarrow \begin{cases}u'=2 \times 2x - 5 \times 1\\v'=1\end{cases}\)
\(\iff \begin{cases}u'=4x - 5\\v'=1\end{cases}\)
\(\iff f'(x) =\frac{(4x - 5)(x+1)-1(2x^2 - 5x + 1)}{(x + 1)^2}\)
\(\iff f'(x) =\frac{4x^2+4x - 5x-5-2x^2+5x-1}{(x + 1)^2}\)
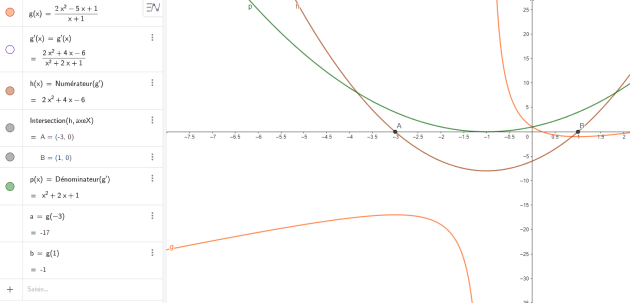
\(\iff f'(x) =\frac{2x^2+4x -6}{(x + 1)^2}\)
Question
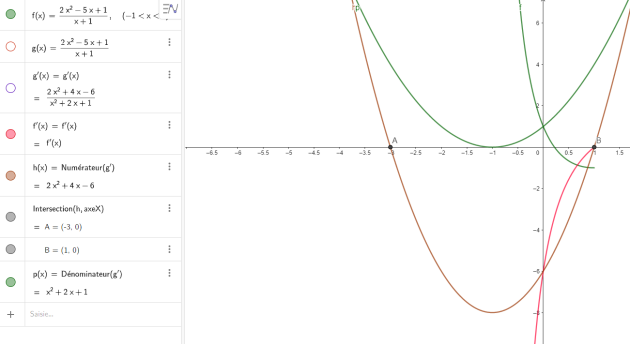
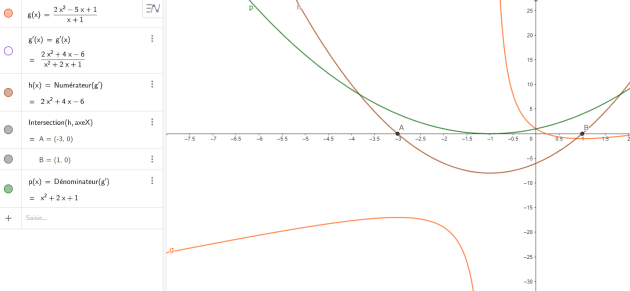
3. Etudier, sur l'intervalle ]-1;+\(\infty\)[ le signe de \(f'(x)\).
Solution
\(f'(x) =\frac{2x^2+4x -6}{(x + 1)^2}\)
Etude du signe du numérateur :
\(2x^2+4x -6=0\)
\(a=2\) \(b=4\) \(c=-6\)
\(\Delta=b^2-4ac=4^2-4 \times 2 \times (-6)\)
\(\iff \Delta=16+48=64\)
Comme \(\Delta>0\), l'équation \(2x^2+4x -6=0\)
admet deux solutions :
\(\begin{cases}x_1=\frac{-b-\sqrt{\Delta}}{2a}\\x_2=\frac{-b+\sqrt{\Delta}}{2a}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{-4-\sqrt{64}}{2 \times 2}\\x_2=\frac{-4+\sqrt{64}}{2 \times 2}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{-4-8}{4}\\x_2=\frac{-4+8}{4}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{-12}{4}\\x_2=\frac{4}{4}\end{cases}\)
\(\iff \begin{cases}x_1=-3\\x_2=1\end{cases}\)
Etude du signe du dénominateur :
\((x + 1)^2>0\) pour tout \(x \in\) ]-1 ;+\(\infty\)[
car le carré d'un nombre réel est toujours positif.
\((x + 1)^2=0 \iff x+1=0 \iff x=-1\)
\(g (-3) =\frac{2 \times (-3)^2 - 5 \times (-3)+ 1}{(-3) + 1}\)
\(\iff g (-3) =\frac{2 \times 9 +15+ 1}{-2}\)
\(\iff g (-3) =\frac{18+15+ 1}{-2}\)
\(\iff g (-3) =\frac{34}{-2}\)
\(\iff g (-3) =-17\)
\(g (1) =\frac{2 \times 1^2 - 5 \times 1+ 1}{1 + 1}\)
\(\iff g (1) =\frac{2 \times 1 -5+ 1}{2}\)
\(\iff g (1) =\frac{2-5+ 1}{2}\)
\(\iff g (1) =\frac{-2}{2}\)
\(\iff g (1) =-1\)
Question
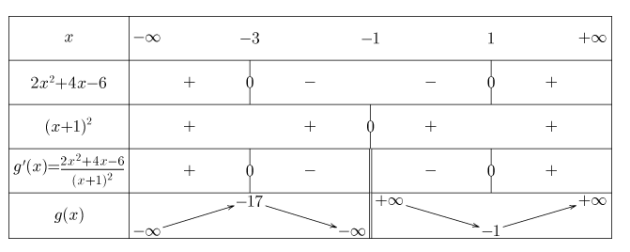
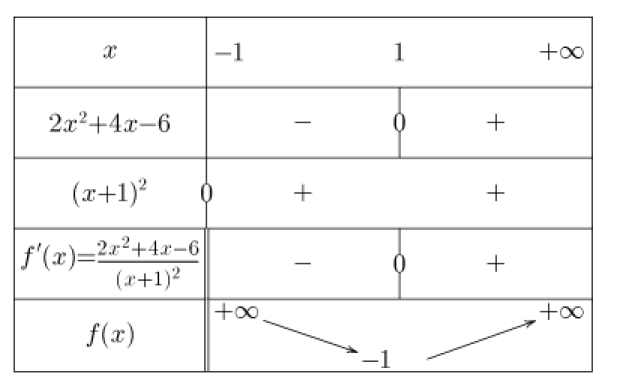
4. En déduire le tableau de variations de la fonction \(f\).
5. On appelle \(C_f\) la courbe représentative de la fonction \(f\) dans un repère orthonormal d'unité
de longueur 2cm.
On note T la tangente à la la courbe \(C_f\) au point d'abscisse 3.
Question
Calculer l'équation réduite de la droite T.
Solution
L'équation réduite de la droite T tangente à la la courbe \(C_f\) au point d'abscisse 3 est :
\(y=f'(3)(x-3)+f(3)\)
\(\iff y=f'(3)(x-3)+f(3)\)
\(f'(3) =\frac{2 \times 3^2+4 \times 3-6}{(3 + 1)^2}\)
\(\iff f'(3) =\frac{2 \times 9+12-6}{4^2}\)
\(\iff f'(3) =\frac{18+12-6}{16}\)
\(\iff f'(3) =\frac{24}{16}\)
\(\iff f'(3) =\frac{3}{2}=1,5\)
\(f (3) =\frac{2 \times 3^2 - 5 \times 3+ 1}{3 + 1}\)
\(\iff f (3) =\frac{2 \times 9 - 15+ 1}{3+ 1}\)
\(\iff f (3) =\frac{18 - 15+ 1}{4}\)
\(\iff f (3) =\frac{4}{4}=1\)
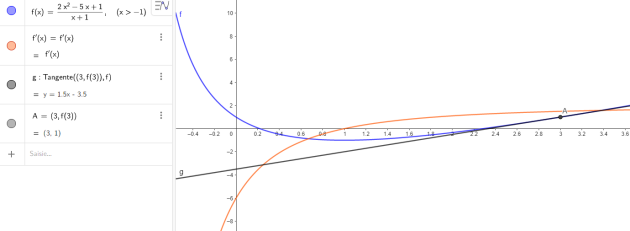
L'équation réduite de la droite T tangente à la la courbe \(C_f\) au point d'abscisse 3 est donc :
\(y=1,5(x-3)+1\)
\(\iff y=1,5x-4,5+1\)
\(\iff y=1,5x-3,5\)
Question
6. a. Compléter le tableau de valeurs suivant avec des valeurs décimales à 0,1 près
\(x\) | -0,5 | 0 | 1 | 1,5 | 2 | 3 | 4 | 6 |
|---|---|---|---|---|---|---|---|---|
\(f(x)\) |
Question
b. Construire la courbe \(C_f\) et la droite T.