Chapitre VII Trigonométrie

• Déterminons la mesure principale de \(- \frac{19\pi}{6}\)

\(\frac{- \frac{19\pi}{6}}{2\pi}=\frac{- \frac{19\pi}{6}}{\frac{2\pi}{1}}\)

\(\iff \frac{- \frac{19\pi}{6}}{2\pi}=- \frac{19\pi}{6} \times \frac{1}{2\pi}\)

\(\iff \frac{- \frac{19\pi}{6}}{2\pi}=- \frac{19}{12}\)

\(- \frac{24}{12} \le- \frac{19}{12}\le - \frac{12}{12}\)

\(\iff - 2 \le-\frac{19}{12}\le -1\)

donc \(-\frac{19\pi}{6}\) est compris entre -1 et -2 tours.

• \(-\frac{19\pi}{6}+1\times 2\pi=-\frac{19\pi}{6}+\frac{12\pi}{6}=-\frac{7\pi}{6}\notin ]-\pi ;pi]\)

• \(-\frac{19\pi}{6}+2\times 2\pi=-\frac{19\pi}{6}+4\pi\)

  \(\iff -\frac{19\pi}{6}+2\times 2\pi=-\frac{19\pi}{6}+\frac{24\pi}{6}=\frac{5\pi}{6}\in ]-\pi ;pi]\)

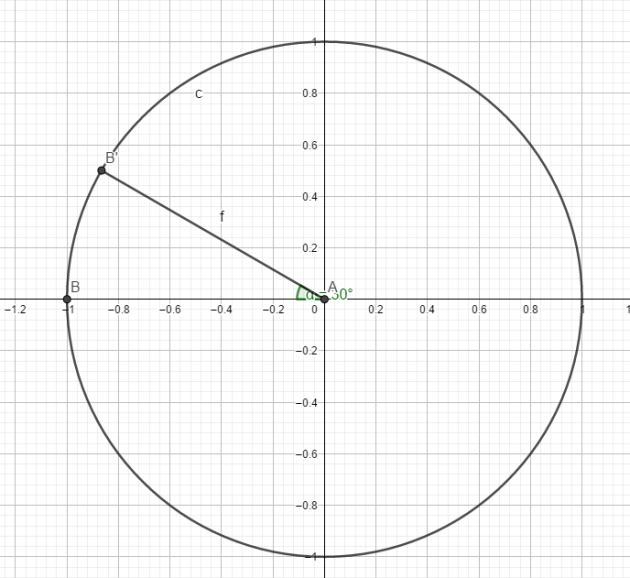
La mesure principale de \(- \frac{19\pi}{6}\) est donc \(\frac{5\pi}{6}\)

donc sin(\(- \frac{19\pi}{6}\))=sin(\(\frac{5\pi}{6}\))=\(\frac{1}{2}\)