Exercice : Exercice basique 2
On donne la figure suivante :
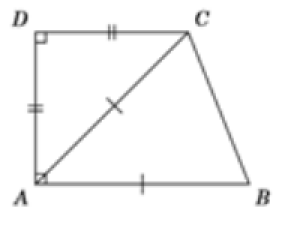
Déterminer une mesure en radians des angles suivants :
Question
\(1. (\vec{AC},\vec{AD})\)
Solution
Le triangle ADC est isocèle rectangle en D donc
\((\vec{AC},\vec{AD})=(\vec{CD},\vec{CA})\)
La somme des mesures des angles d'un triangle vaut \(\pi\)(180°)
donc
\(2(\vec{AC},\vec{AD})+\frac{\pi}{2}=\pi\)
\(\iff 2(\vec{AC},\vec{AD})=\pi-\frac{\pi}{2}\)
\(\iff 2(\vec{AC},\vec{AD})=\frac{\pi}{2}\)
\(\iff (\vec{AC},\vec{AD})=\frac{\pi}{4}\)
Question
\(2. (\vec{CD},\vec{CB})\)
Solution
\((\vec{CD},\vec{CB})=(\vec{CD},\vec{CA})+(\vec{CA},\vec{CB})\)
\((\vec{AB},\vec{AD})=\frac{\pi}{2}\)
\(\iff (\vec{AB},\vec{AC})+(\vec{AC},\vec{AD})=\frac{\pi}{2}\)
\(\iff (\vec{AB},\vec{AC})=\frac{\pi}{2}-(\vec{AC},\vec{AD})\)
\(\iff (\vec{AB},\vec{AC})=\frac{\pi}{2}-\frac{\pi}{4}\)
\(\iff (\vec{AB},\vec{AC})=\frac{\pi}{4}\)
\((\vec{AB},\vec{AC})+(\vec{BC},\vec{BA})+(\vec{CA},\vec{CB})=\pi\)
\(\iff \frac{\pi}{4}+2(\vec{CA},\vec{CB})=\pi\)
\(\iff 2(\vec{CA},\vec{CB})=\pi-\frac{\pi}{4}\)
\(\iff 2(\vec{CA},\vec{CB})=\frac{3\pi}{4}\)
\(\iff (\vec{CA},\vec{CB})=\frac{3\pi}{8}\)
\((\vec{CD},\vec{CB})=(\vec{CD},\vec{CA})+(\vec{CA},\vec{CB})\)
\(\iff (\vec{CD},\vec{CB})=\frac{\pi}{4}+\frac{3\pi}{8}\)
\(\iff (\vec{CD},\vec{CB})=\frac{2\pi}{8}+\frac{3\pi}{8}\)
\(\iff (\vec{CD},\vec{CB})=\frac{5\pi}{8}\)
Question
\(3. (\vec{BC},\vec{DA})\)
Solution
\((\vec{BC},\vec{DA})=(\vec{BC},\vec{BA})+(\vec{BA},\vec{DA})\)
\(\iff (\vec{BC},\vec{DA})=\frac{5\pi}{8}+\frac{\pi}{2}\)
\(\iff (\vec{BC},\vec{DA})=\frac{5\pi}{8}+\frac{4\pi}{8}=\frac{9\pi}{8}\)