Exercice : Exercice basique 6
Question
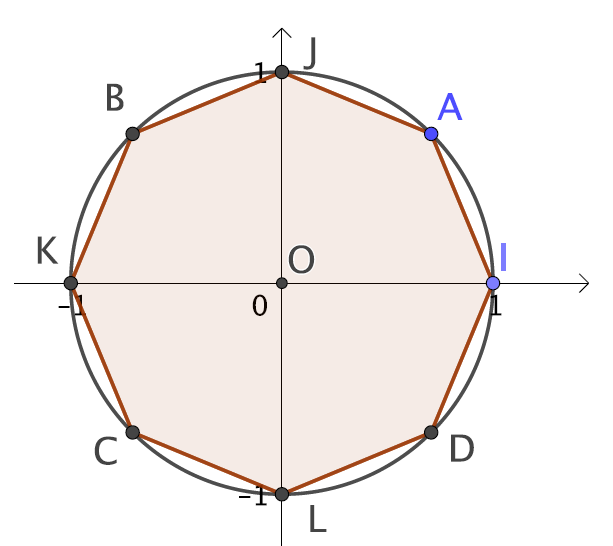
Compléter les tableaux suivants sans justifier :
\(x\) | \(\frac{\pi}{4}\) | \(\pi\) | \(-\frac{17\pi}{2}\) | |||
|---|---|---|---|---|---|---|
Point-image | B | C | ||||
\(\cos(x)\) | \(\frac{\sqrt{2}}{2}\) | -1 | ||||
\(\sin(x)\) |
Solution
\(x\) | \(\frac{\pi}{4}\) | \(\pi\) | \(-\frac{17\pi}{2}\) | \(\frac{3\pi}{4}\) | \(\frac{-3\pi}{4}\) | \(\pi\) |
|---|---|---|---|---|---|---|
Point-image | A | K | L | B | C | K |
\(\cos(x)\) | \(\frac{\sqrt{2}}{2}\) | -1 | 0 | -\(\frac{\sqrt{2}}{2}\) | \(-\frac{\sqrt{2}}{2}\) | -1 |
\(\sin(x)\) | \(\frac{\sqrt{2}}{2}\) | 0 | -1 | \(\frac{\sqrt{2}}{2}\) | \(-\frac{\sqrt{2}}{2}\) | 0 |
Question
Angle | \(\widehat{IOA}\) | \(\widehat{AOK}\) | \(\widehat{IAO}\) |
|---|---|---|---|
Mesure en radians | |||
Mesure en ° |
Solution
Angle | \(\widehat{IOA}\) | \(\widehat{AOK}\) | \(\widehat{IAO}\) |
|---|---|---|---|
Mesure en radians | \(\frac{\pi}{4}\) | \(\frac{3\pi}{4}\) | \(\frac{3\pi}{8}\) |
Mesure en ° | 45° | 135° | 67,5° |
\(\widehat{IAO}+\widehat{OIA}+\widehat{AOI}=\pi\)
\(\iff 2\widehat{IAO}+\widehat{AOI}=\pi\)
\(\iff 2\widehat{IAO}+\frac{\pi}{4}=\pi\)
\(\iff 2\widehat{IAO}=\pi-\frac{\pi}{4}\)
\(\iff \widehat{IAO}=\frac{3\pi}{8}\)
Question
3. Quelle est la longueur de l'arc \(\stackrel{\frown}{IA}\)? Celle de l'arc \(\stackrel{\frown}{CD}\)?
Solution
La longueur de l'arc \(\stackrel{\frown}{IA}\) est \(\frac{\pi}{4}\)
La longueur de l'arc \(\stackrel{\frown}{CD}\) est \(\frac{\pi}{2}\)
Question
4.Tracer dans le triangle OAI la hauteur [AH] issue de A puis en déterminer la longueur.
Solution
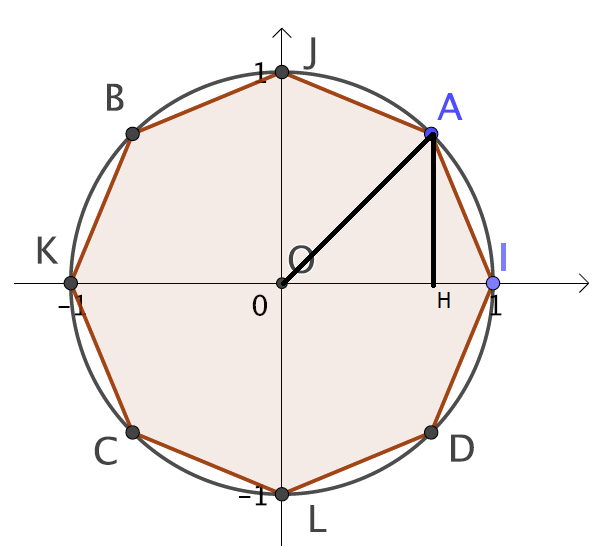
Le triangle OHA est isocèle rectangle en H d'hypoténuse [OA].
\(OH^2+AH^2=OA^2\)
\(\iff OH^2+AH^2=1^2\)
\(\iff 2AH^2=1\)
\(\iff AH^2=\frac{1}{2}\)
\(\iff AH=\sqrt{\frac{1}{2}}\)
\(\iff AH=\frac{\sqrt{1}}{\sqrt{2}}\)
\(\iff AH=\frac{1}{\sqrt{2}}\)
\(\iff AH=\frac{\sqrt{2}}{\sqrt{2}^2}\)
\(\iff AH=\frac{\sqrt{2}}{2}\)
\(\iff AH=sin(\frac{\pi}{4})=\frac{\sqrt{2}}{2}\)
Question
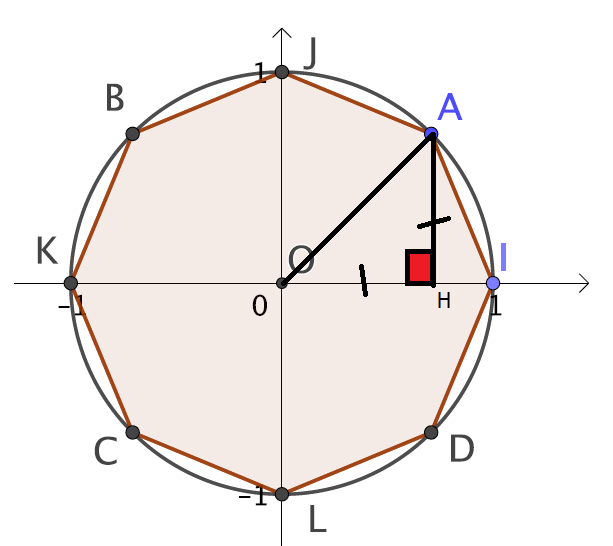
5.En déduire l'aire du triangle OAI puis celle de l'octogone IAJBKCLD.
Solution
L'aire du triangle OAI est donc :
\(\frac{base\times hauteur}{2}=\frac{1 \times \frac{\sqrt{2}}{2}}{2}=\frac{\sqrt{2}}{4}\)
L'aire de l'octogone IAJBKCLD est :
\(8\times \frac{\sqrt{2}}{4}=2\sqrt{2}\simeq2,83\)