Exercice : Exercice basique 8
Question
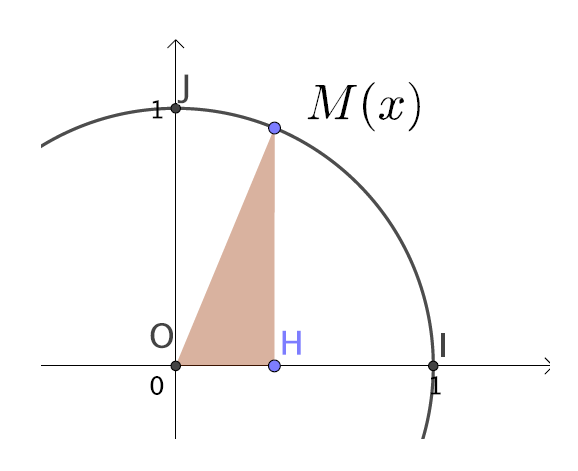
1. En vous appuyant sur la figure ci-dessus, tracée dans le cercle trigonométrique, compléter ET redémontrer le résultat du cours suivant : \(\cos^{2}(x)+\sin^{2}(x)=...........\)
Solution
D'après le théorème de Pythagore dans le triangle OHM,
rectangle en H d'hypoténuse OM :
\(OM^2=OH^2+HM^2\)
\(\iff 1^2=cos^2 x+sin^2 x\)
\(\iff cos^2 x+sin^2 x=1\)
Question
2. Sachant que \(\cos(\frac{\pi}{8})=\dfrac{\sqrt{2+\sqrt{2}}}{2}\)
déterminer \(\cos(-\frac{\pi}{8})\)
ainsi que \(\cos^{2}(-\frac{\pi}{8})\).
Solution
\(\cos(-\frac{\pi}{8})=\dfrac{\sqrt{2+\sqrt{2}}}{2}\)
car \(cos(x)=cos(-x)\)
\(\cos^{2}(-\frac{\pi}{8})=(\dfrac{\sqrt{2+\sqrt{2}}}{2})^2\)
\(\iff \cos^{2}(-\frac{\pi}{8})=\dfrac{(\sqrt{2+\sqrt{2}})^2}{4}\)
\(\iff \cos^{2}(-\frac{\pi}{8})=\dfrac{2+\sqrt{2}}{4}\)
Question
3. En déduire la valeur exacte de \(\sin^{2}(-\frac{\pi}{8})\) puis celle de \(\sin(-\frac{\pi}{8}).\)
Solution
\(\cos^{2}(x)+\sin^{2}(x)=1\)
\(\iff \cos^{2}(-\frac{\pi}{8})+\sin^{2}(-\frac{\pi}{8})=1\)
\(\iff \sin^{2}(-\frac{\pi}{8})=1-\cos^{2}(-\frac{\pi}{8})\)
\(\iff \sin^{2}(-\frac{\pi}{8})=1-(\dfrac{2+\sqrt{2}}{4}\)
\(\iff \sin^{2}(-\frac{\pi}{8})=\frac{4}{4}-(\dfrac{2+\sqrt{2}}{4}\)
\(\iff \sin^{2}(-\frac{\pi}{8})=\frac{4-(2+\sqrt{2})}{4}\)
\(\iff \sin^{2}(-\frac{\pi}{8})=\frac{2-\sqrt{2}}{4}\)
\(\iff \sin(-\frac{\pi}{8})=\sqrt{\frac{2-\sqrt{2}}{4}}\)
\(\iff \sin(-\frac{\pi}{8})=\frac{\sqrt{2-\sqrt{2}}}{2}\)