Exercice : Exercice basique 9
Soit \(f\) la fonction définie sur l'ensemble des nombres réels \(\mathbb{R}\) par :
\(f(x)=\cos(2x)+\cos(x)\sin(x)\)
1. Compléter avec les valeurs exactes :
Question
\(\cos(\frac{\pi}{2})\)=
Solution
\(\cos(\frac{\pi}{2})\)=0
Question
\(\cos(\frac{\pi}{4})\)=
Solution
\(\cos(\frac{\pi}{4})=\frac{\sqrt{2}}{2}\)
Question
\(\sin(\frac{\pi}{4})\)=
Solution
\(\sin(\frac{\pi}{4})=\frac{\sqrt{2}}{2}\)
Question
En déduire que \(f(\frac{\pi}{4})=\frac{1}{2}\)
Solution
\(f(\frac{\pi}{4})=\cos(2\frac{\pi}{4})+\cos(\frac{\pi}{4})\sin(\frac{\pi}{4})\)
\(\iff f(\frac{\pi}{4})=\cos(\frac{\pi}{2})+\cos(\frac{\pi}{4})\sin(\frac{\pi}{4})\)
\(\iff f(\frac{\pi}{4})=0+\frac{\sqrt{2}}{2}\times \frac{\sqrt{2}}{2}\)
\(\iff f(\frac{\pi}{4})=\frac{\sqrt{2} \times \sqrt{2}}{4}\)
\(\iff f(\frac{\pi}{4})=\frac{2}{4}=\frac{1}{2}\)
Question
2. De même, compléter avec les valeurs exactes :
Question
\(\cos(\frac{\pi}{3})\)=
Solution
\(\cos(\frac{\pi}{3})=\frac{1}{2}\)
Question
\(\cos(\frac{\pi}{6})\)=
Solution
\(\cos(\frac{\pi}{6})=\sqrt{3}{2}\)
Question
\(\sin(\frac{\pi}{6})\)=
Solution
\(\sin(\frac{\pi}{6})=\frac{1}{2}\)
Question
En déduire que \(f(\frac{\pi}{6})=\frac{2+\sqrt{3}}{4}\)
Solution
\(f(\frac{\pi}{6})=\cos(2\frac{\pi}{6})+\cos(\frac{\pi}{6})\sin(\frac{\pi}{6})\)
\(\iff f(\frac{\pi}{6})=\cos(\frac{\pi}{3})+\cos(\frac{\pi}{6})\sin(\frac{\pi}{6})\)
\(\iff f(\frac{\pi}{6})=\frac{1}{2}+\frac{\sqrt{3}}{2} \times \frac{1}{2}\)
\(\iff f(\frac{\pi}{6})=\frac{2+\sqrt{3}}{4}\)
Question
3. Déterminer de même \(f(\frac{\pi}{2})\) et \(f(\pi)\)
Solution
\(f(\frac{\pi}{2})=\cos(2\frac{\pi}{2})+\cos(\frac{\pi}{2})\sin(\frac{\pi}{2})\)
\(\iff f(\frac{\pi}{2})=\cos(\pi)+0\)
\(\iff f(\frac{\pi}{2})=-1\)
\(f(\pi)=\cos(2\pi)+\cos(\pi)\sin(\pi)\)
\(\iff f(\pi)=1+0\)
\(\iff f(\pi)=1\)
Question
4. Rappeler la définition : « On dit qu'une fonction \(g\) est périodique de période T si, pour tout \(x\in\mathbb{R}\), \(g(x+.....)=\)g(............)»
Solution
\(g\) est périodique de période T si, pour tout \(x\in\mathbb{R}\),
\(g(x+T)=g(x)\)
Question
5. Démontrer que la fonction \(f\) est périodique de période \(\pi\)
Solution
\(f(x+\pi)=\cos(2(x+\pi))+\cos(x+\pi)\sin(x+\pi)\)
\(\iff f(x+\pi)=\cos(2x+2\pi)+(-\cos(x))(-\sin(x))\)
\(\iff f(x+\pi)=\cos(2x)+\cos(x)\sin(x)\)
\(\iff f(x+\pi)=f(x)\)
La fonction \(f\) est périodique de période \(\pi\)
Question
6. Déduire des questions précédentes la valeur de \(f(\frac{7\pi}{6})\) et celle de \(f(\frac{31\pi}{6}) .\)
Solution
\(f(\frac{7\pi}{6})=f(\frac{\pi}{6}+\pi)=f(\frac{\pi}{6})=\frac{2+\sqrt{3}}{4}\)
\(f(\frac{31\pi}{6})=f(\frac{30\pi}{6}+\frac{\pi}{6})=f(5\pi+\frac{\pi}{6})=f(\frac{\pi}{6})=\frac{2+\sqrt{3}}{4}\)
Question
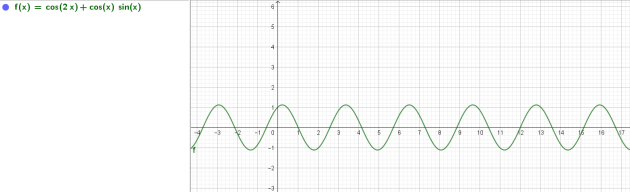
7. Tracer , à l'aide de Geogebra, la courbe représentative de la fonction \(f\).
Celle-ci semble-t-elle symétrique par rapport à l'axe des ordonnées? ...........
En déduire une propriété que la fonction \(f\) possède ou ne possède pas :.....................................................
Solution
La courbe n'est pas symétrique par rapport à l'axe des ordonnées. La fonction n'est donc pas paire.
\(f(-x)=\cos(2(-x))+\cos(-x)\sin(-x)\)
\(f(-x)=\cos(-2x)+\cos(x)(-\sin(x))\)
\(f(-x)=\cos(2x)-\cos(x)\sin(x)\ne f(-x)\) La fonction n'est donc pas paire.
\(f(-x)\ne -f(x)\) La fonction n'est donc pas impaire.