Exercice : Exemple 1
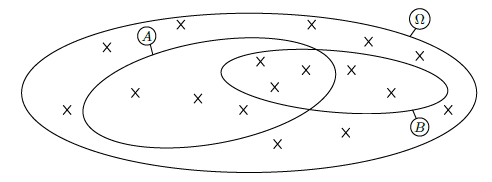
On considère un ensemble Ω et deux de ses parties A et B représentés ci-dessous et dont les éléments sont représentés par des croix :
De manière équiprobable, on choisit un élément au hasard.
Question
1. a. Quelle est la probabilité que l'élément tiré appartiennent à A?
Solution
La probabilité que l'élément tiré appartiennent à A est de \(\frac{6}{17}\)
Question
b. Sachant qu'on a tiré un élément de B, quelle est la probabilité que cet élément appartiennent à A on note \(p_B(A)\)?
Solution
On a tiré un élément de B, la probabilité que cet élément appartiennent à A est de \(\frac{3}{5}\)
Question
2. a. Déterminer les probailité suivantes : \(P(B) ; P(A \cap B)\)
Solution
\(P(B)=\frac{5}{17}\)
\(P(A \cap B)=\frac{3}{17}\)
Question
b. Donner la valeur du quotient \(\frac{P(A \cap B)}{P(B)}\)
Solution
\(\frac{P(A \cap B)}{P(B)}=\frac{\frac{3}{17}}{\frac{5}{17}}=\frac{3}{17}\times\frac{17}{5}=\frac{3}{5}\)
On remarque que \(\color{red}p_B(A)=\frac{P(A \cap B)}{P(B )}\)