Exercice : Exemple 13
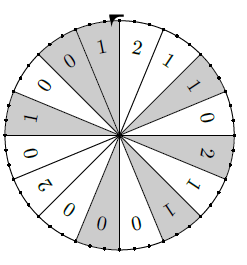
Un jeu consiste à faire tourner la roue ci-contre une première fois et de noter la couleur de la case obtenue, puis de faire tourner la roue une seconde fois et de noter le nombre obtenu.
Les deux lancers de la roue sont évidemment indépendants entre eux.
On considère les deux événements :
A : “la case obtenue est grise lors du premier tirage” ;
B : “la case obtenue porte le numéro 0 lors du second tirage”.
Question
1. Justifier que :\( P_A(B) = P(B)\)
Solution
\(P_A(B) = P(B)\) car les deux lancers de la roue sont indépendants : le premier lancer n'influence pas le résultat du deuxième lancer.
Question
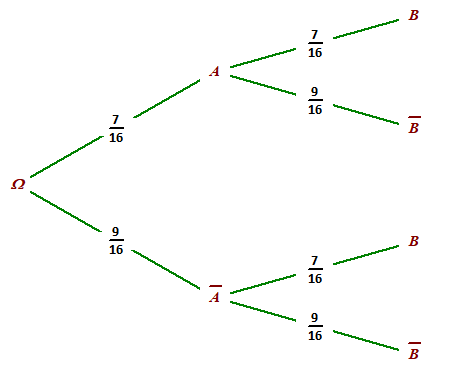
2. Dresser un arbre de probabilité représentant ce jeu.
Question
3. Calculer la probabilité \(P_A(B)\)
Solution
Par le calcul :
\(P_A(B) = \frac{P(A \cap B)}{P(A)}\)
\(P(A \cap B)=\frac{7}{16} \times \frac{7}{16}\)
\(P_A(B) = \frac{P(A \cap B)}{P(A)}=\frac{\frac{7}{16}\times\frac{7}{16}}{\frac{7}{16}}=\frac{7}{16} =P(B)\)