Exercice : Exemple 21
Chaque jour où il travaille, Paul doit se rendre à la gare pour rejoindre son lieu de travail en train.
Pour cela, il prend son vélo deux fois sur trois et, s'il ne prend pas son vélo, il prend sa voiture.
Lorsqu'il prend son vélo pour rejoindre la gare, Paul ne rate le train qu'une fois sur 50 alors que, lorsqu'il prend sa voiture pour rejoindre la gare Paul rate son train une fois sur 10.
On considère une journée au hasard lors de laquelle Paul ira à la gare pour prendre le train qui le conduira au travail.
On note :
V l'évènement “Paul prend son vélo pour rejoindre la gare” ;
R l'évènement “Paul rate son train”.
Question
1. Représenter la situation par un arbre pondéré.
Solution
V l'évènement “Paul prend son vélo pour rejoindre la gare” ;
R l'évènement “Paul rate son train”.
donc
\(\overline{V}\) l'évènement “Paul prend sa voiture pour rejoindre la gare” ;
\(\overline{R}\) l'évènement “Paul ne rate pas son train”.
D'après l'énoncé :
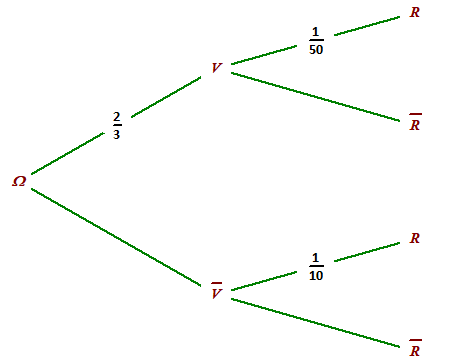
Calcul des valeurs manquantes :
\(p(\overline{V})=1-p(V)\)
\(\iff p(\overline{V})=1-\frac{2}{3}\)
\(\iff p(\overline{V})=\frac{3}{3}-\frac{2}{3}\)
\(\iff p(\overline{V})=\frac{1}{3}\)
\(p_V(R)+p_V(\overline{R})=1\)
\(\iff \frac{1}{50}+p_V(\overline{R})=1\)
\(\iff p_V(\overline{R})=1-\frac{1}{50}\)
\(\iff p_V(\overline{R})=\frac{50}{50}-\frac{1}{50}\)
\(\iff p_V(\overline{R})=\frac{49}{50}\)
\(p_{\overline{V}}(R)+p_{\overline{V}}(\overline{R})=1\)
\(\iff \frac{1}{10}+p_{\overline{V}}(\overline{R})=1\)
\(\iff p_{\overline{V}}(\overline{R})=1-\frac{1}{10}\)
\(\iff p_{\overline{V}}(\overline{R})=\frac{10}{10}-\frac{1}{10}\)
\(\iff p_{\overline{V}}(\overline{R})=\frac{9}{10}\)
On en déduit l'arbre de probabilité suivant :
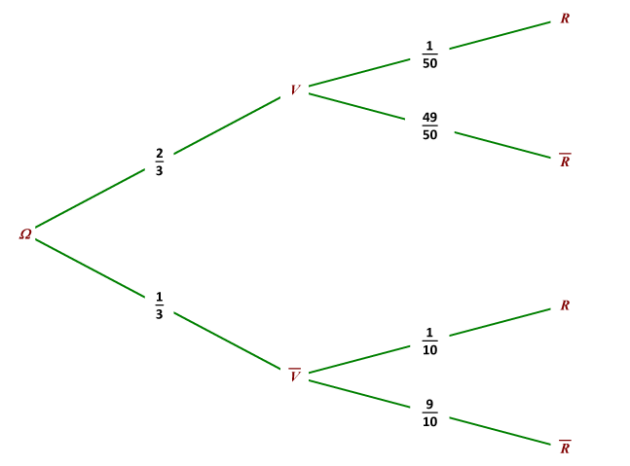
Question
2. Calculer \(p(V \cap R)\) et interpréter cette valeur.
Solution
Calcul de la probabilité que Paul soit venu en train et ait raté son train :
\(p_V(R)=\frac{p(V \cap R)}{p(V)}\)
\(\iff p(V \cap R)= p_V(R) \times p(V)\)
\(\iff p(V \cap R)= \frac{1}{50} \times \frac{2}{3}= \frac{1}{25} \times \frac{1}{3}=\frac{1}{75}\)
Question
3. Quelle est la probabilité que Paul rate son train?
Solution
Calcul de la probabilité que Paul ait raté son train :é
Calcul de la probabilité que Paul soit venu en vélo et ait raté son train :
\(p_{\overline{V}}(R)=\frac{p(\overline{V} \cap R)}{p(\overline{V})}\)
\(\iff p({\overline{V}} \cap R)= p_{\overline{V}}(R) \times p(\overline{V})\)
\(\iff p({\overline{V}} \cap R)= \frac{1}{10} \times \times \frac{1}{3}\)
\(\iff p({\overline{V}} \cap R)= \frac{1}{30}\)
Finalement :
\(p(R)=\frac{1}{75}+ \frac{1}{30}\)
\(\iff p(R)=\frac{2}{150}+ \frac{5}{150}\)
\(\iff p(R)=\frac{7}{150}\)
La probabilité que Paul rate son train est : \(\frac{7}{150}\)
Question
4. Paul a raté son train, quelle est la probabilité qu'il soit venu à la gare à vélo ?
Solution
Calcul de la probabilité que Paul soit venu à la gare à vélo, sachant qu'il a raté son train :
\(p_R(V)=\frac{p(V\cap R)}{p(R)}=\frac{\frac{1}{75}}{\frac{7}{150}}=\frac{1}{75} \times \frac{150}{7}\)
\(p_R(V)=\frac{p(V\cap R)}{p(R)}=\frac{1}{1} \times \frac{2}{7}=\frac{2}{7}\)