Exercice : Exemple 2
Un jeu consiste à secouer et renverser une bouteille afin d'en sortir un de ses éléments.
Voici le contenu de cette bouteille :
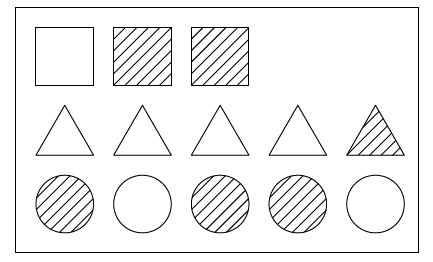
1.Déterminer la probabilité des évènements suivants :
Question
a. A : “L'élément sorti est un carré” ;
Solution
p(A)=\(\frac{3}{13}\) : “L'élément sorti est un carré” ;
Question
b. B : “L'élément sorti est rayé” ;
Solution
\(p(B)= \frac{6}{13}\) : “L'élément sorti est rayé” ;
Question
c. \(A \cap B\) : “L'élément sorti est un carré rayé”.
Solution
\(p(A \cap B)=\frac{2}{13}\) : “L'élément sorti est un carré rayé”.
Question
2. a. Sachant qu'un carré est sorti, quelle est la probabilité pour qu'il soit rayé ? On note cette probabilité \(P_A(B)\)
Solution
Sachant qu'un carré est sorti, quelle est la probabilité pour qu'il soit rayé : \(P_A(B)=\frac{2}{3}\)
Question
b. Vérifier l'égalité suivante : \(P_A(B) =\frac{P(A \cap B)}{P(A)}\)
Solution
\(\frac{P(A \cap B)}{P(A)}=\frac{\frac{2}{13}}{\frac{3}{13}}=\frac{2}{13}\times \frac{13}{3}=\frac{2}{3}\)
donc \(\color{red}{P_A(B) =\frac{P(A \cap B)}{P(A)}}\)
Question
3. a. Sachant que l'élément sorti est rayé, quelle est la probabilité pour que ce soit un carré ?
On note cette probabilité \(P_B(A)\)
Solution
Sachant que l'élément sorti est rayé, la probabilité pour que ce soit un carré est : \(P_B(A)=\frac{2}{6}=\frac{1}{3}\)
Question
b. Vérifier l'égalité suivante : \(P_B(A) =\frac{P(A \cap B)}{P(B)}\)
Solution
\(\frac{P(A \cap B)}{P(B)}=\frac{\frac{2}{13}}{\frac{6}{13}}=\frac{2}{13}\times \frac{16}{6}=\frac{2}{6}=\frac{1}{3}\)
donc \(\color{red}{P_B(A) =\frac{P(A \cap B)}{P(B)}}\)