Exercice : Exemple 10
Dans un espace probabilisé, on considère deux évènements A et B.
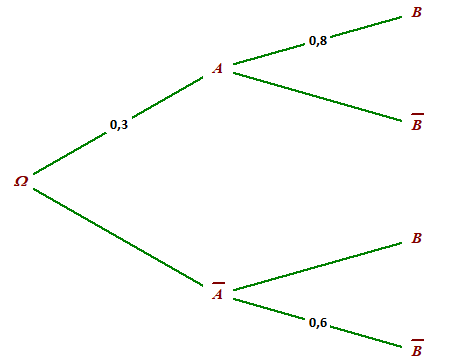
On connait les probabilités suivantes : P(A) = 0,3 ; \(P_A(B) = 0,8\) ; \(P_{\overline{A}}(\overline{B}) = 0,6\)
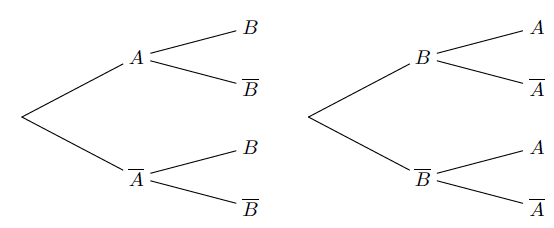
Question
Compléter, si nécessaire avec des valeurs arrondies au centième, les deux arbres de probabilité ci-dessus.
Solution
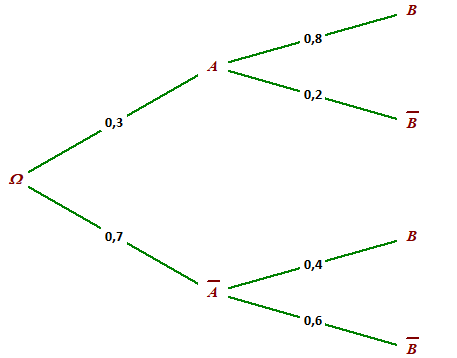
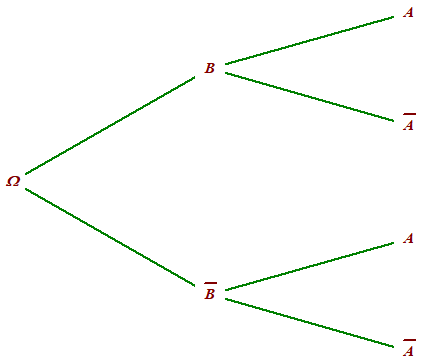
P(A) = 0,3 ;
\(P_A(B) = 0,8=\frac{P(A\cap B)}{P(A)}=\frac{P(A\cap B)}{0,3}\)
\(P(A\cap B)=0,8 \times 0,3=0,24\)
\(\color{red}{P(A\cap B)}=0,24\)
\(P_{\overline{A}}(\overline{B}) =1-P_{\overline{A}}(B)= 0,6\)
donc \(1-P_{\overline{A}}(B)= 0,6\)
\(1-P_{\overline{A}}(B)= 0,6\)
\(-P_{\overline{A}}(B)= 0,6-1=-0,4\)
\(\color{red}{P_{\overline{A}}(B)=0,4}\)
\(P_{\overline{A}}(B)=0,4=\frac{P(\overline{A} \cap B)}{P(\overline{A})}=\frac{P(\overline{A} \cap B)}{1-P(A)}=\frac{P(\overline{A} \cap B)}{1-0,3}=\frac{P(\overline{A} \cap B)}{0,7}\)
\(P(\overline{A} \cap B)=0,4 \times 0,7=0,28\)
\(P(B)=P(A\cap B)+P(\overline{A} \cap B)=0,24+0,28=0,52\)
\(\color{red}{P(B)=0,52}\) par la formule des probabilités totales.
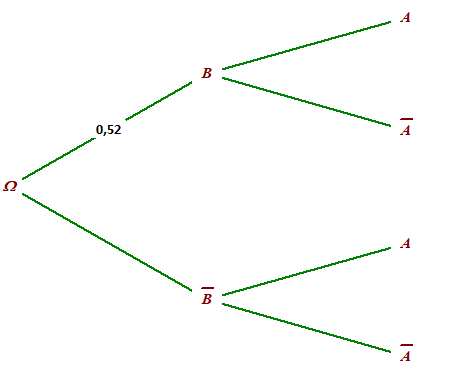
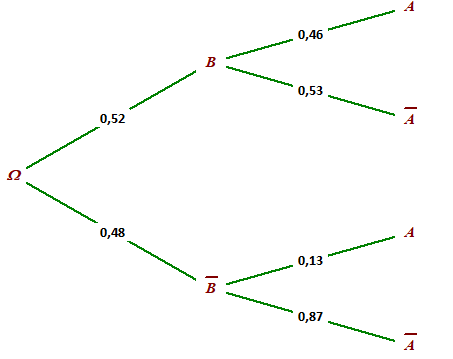
\(P_{B}(A)= \frac{P(A \cap B)}{P(B)}=\frac{0,24}{0,52}\simeq0,46\)
\(P_{B}(\overline{A})=1-P_{B}(A)\simeq0,54\)
\(P(A)=P(A\cap B)+P(A \cap \overline{B})=0,24+P(A \cap \overline{B})=0,3\) par la formule des probabilités totales.
donc\( P(A \cap \overline{B})=0,3-0,24=0,06\)
\(P_{\overline{B}}(A)= \frac{P(A) \cap \overline{B}}{\overline{B}}=\frac{0,06}{1-0,52}\simeq0,13\)
et donc \(P_{\overline{B}}(A)=1-P_{B}(A)\simeq 1-0,13\simeq0,87\)