Exercice : Exemple 9
Dans un espace probabilisé, on considère les deux évènements A et B vérifiant les conditions suivantes :
\(P(A) = 0,64 ; P_A(B) = 0,3 ; P_{\overline{A}}(B) = 0,5\)
Question
1. Construire un arbre de probabilité représentant cette situation.
Solution
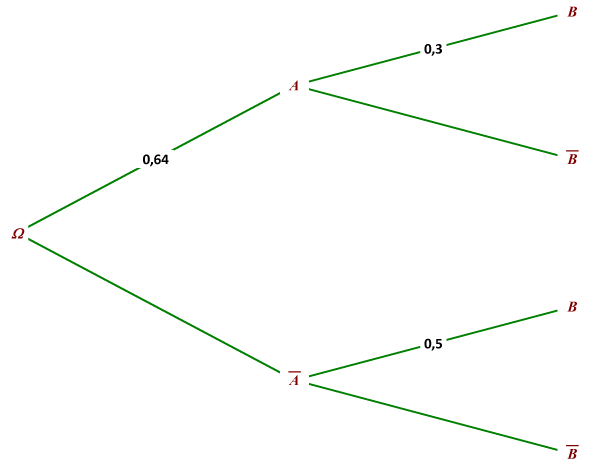
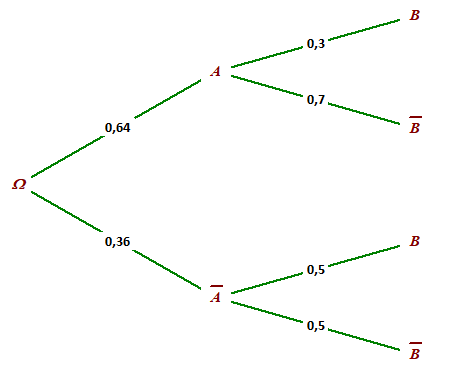
On complète les branches car la somme des probabilités partant d'un noeud sont égales à 1.
Question
2. a. Déterminer les probabilités des évènements suivants : \(P(A \cap B) ; P(\overline{A} \cap B)\)
Solution
\(p(A \cap B)=p(A) \times p_A(B)= 0,64 \times 0,3=0,192\) car les probabilités situées sur un même chemin se multiplient.
\(P(\overline{A} \cap B)=p(\overline{A}) \times p_{\overline{A}}(B)=0,36 \times 0,5=0,18\) car les probabilités situées sur un même chemin se multiplient.
Question
b. A l'aide de la formule des probabilités totale, déterminer la probabilité de l'événement B.
Solution
\(b. p(B)=P(A \cap B)+P(\overline{A} \cap B)=0,192+0,18\) grâce à la formule des probabilités totales