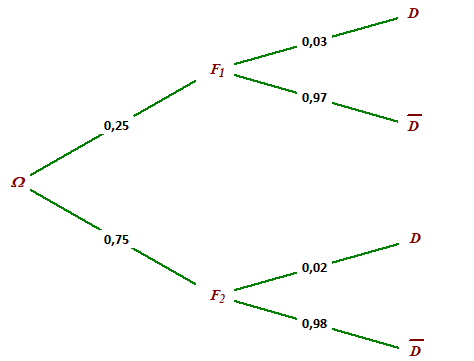
Exercice : Exemple 11
Un responsable de magasin achète des composants électroniques auprès de deux fournisseurs dans les proportions suivantes : 25% au premier fournisseur et 75% au second.
La proportion de composants défectueux est de 3% chez le premier fournisseur et de 2% chez le second.
On note :
D : l'évènement “le composant est défectueux” ; (\(\overline{D}\) le composant n'est pas défectueux)
\(F_1\) : l'évènement “le composant provient du premier fournisseur”;
\(F_2\) : l'évènement “le composant provient du second fournisseur”.
Question
1. Dresser un arbre de probabilité correspondant à cette situation.
Question
2. Calculer \(P(D \cap F_1)\), puis démontrer que P(D)=0,0225 grâce à la formule des probabilités totales.
Solution
\(P(D \cap F_1)=P(F_1) \times P_{F_1}(D)=0,25 \times 0,03=0,0075\)
\(P(D \cap F_2)=P(F_2) \times P_{F_2}(D)=0,75 \times 0,02=0,0150\)
\(P(D)=P(D \cap F_1)+P(D \cap F_2)=0,075+0,0150=\)0,0225 grâce à la formule des probabilités totales.
Question
3. Sachant qu'un composant est défectueux, quelle est la probabilité qu'il provienne du premier fournisseur ? Utiliser la formule des probabilités conditionnelles.
On arrondira cette valeur au millième près.
Solution
\(P_D(F_1)=\frac{P(F_1 \cap D)}{P{D}}=\frac{0,0075}{0,0225}\simeq0,333\)
Si un composant est défectueux, la probabilité qu'il provienne du premier fournisseur est de 33,3% environ.