Exercice : Exemple 8
Pour trouver une plage et aller se baigner, les touristes ne peuvent choisir qu'entre deux plages, l'une à l'Est et l'autre à l'Ouest.
Un touriste se retrouve deux jours consécutifs en haut de la falaise.
Le premier jour, il choisit au hasard l'une des deux directions.
Le second jour, on admet que la probabilité qu'il choisisse une direction opposée à celle prise la veille vaut 0,8.
Pour i=1 ou i=2, on note \(E_i\) l’événement : “Le touriste se dirige vers l'Est le i-ème jour”
et \(O_i\) l’événement : “Le touriste se dirige vers l'Ouest le i-ème jour”.
Question
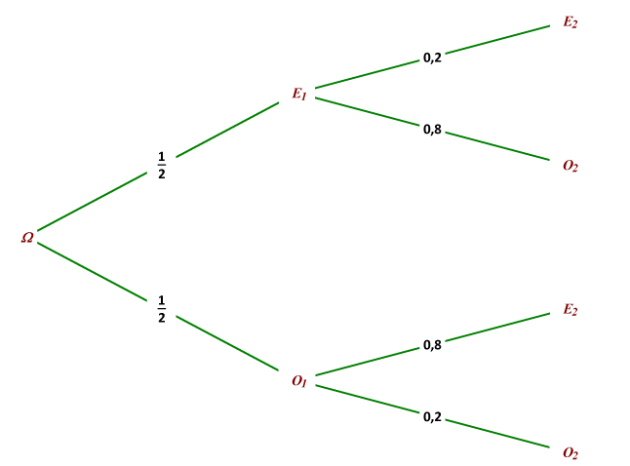
1. Dresser un arbre de probabilités décrivant la situation.
Question
2. Déterminer les probabilités suivantes :
\(P(E_1) ; P_{E1}(O_2) ; P(E_1 \cap E_2).\)
Solution
\(\color{red}{P(E_1)=\frac{1}{2}}\) car le choix de la première plage est équiprobable.
\(\color{red}{PE_1 (O_2)=0,8}\) car le second jour, on admet que la probabilité qu'il choisisse une direction opposée à celle prise la veille vaut 0,8.
or \(p_{E_1}(E_2) + p_{E_1}(\overline{E_2})=1\)
donc \(p_{E_1}(E_2) +0,8=1\)
\(\color{red}{p_{E_1}(E_2) =1-0,8=0,2}\)
La probabilité d'un chemin est le produit des probabilités des différentes branches qui constituent ce chemin :
\(P(E_1 \cap E_2)=\frac{1}{2}\times 0,2=0,1\)
\(P(O_1 \cap O_2)=\frac{1}{2}\times 0,2=0,1\)
Question
3. Calculer la probabilité que ce touriste se rende sur la même plage deux jours consécutifs.
Solution
La probabilité que ce touriste se rende sur la même plage deux jours consécutifs :
\(P(E_1 \cap E_2)+P(O_1 \cap O_2)=0,1+0,1=0,2\)