Chapitre IX Probabilités Conditionnelles

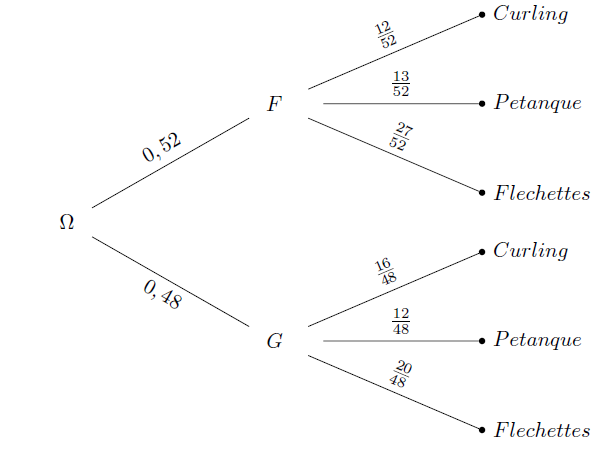
Sur chaque branche de l'arbre, la probabilité se rapporte à l'univers du noeud précédent;

ainsi, la probabilité \(\frac{12}{52}\) est la probabilité de choisir une joueuse de curling parmi les filles

(l'univers de référence est l'ensemble des filles).

Les événements G : "choisir un garçon" et F :"chosir une fille" forment une partition de \(\Omega\) car :

— ils sont deux à deux disjoints : un élève choisi ne peut pas être en même temps un garçon et une fille;

— leur réunion forme \(\Omega\) : un élève choisi ne peut  être qu'un garçon ou une fille.

Cela signifie que chaque issue de \(\Omega\) appartient à un et un seul de ces évènements.

\(p(C) = p(C \cap F) + p(C \cap G) = 0,52 \times \frac{12}{52} + 0,48 \times \frac{16}{48}\)

\(p(C) = 0,12 + 0,16 = 0,28\)

La probabilité qu'un adhérent choisi au hasard pratique le curling est 0,28.