Exercice : Exemple 6
Dans le Lycée Bacanpauch :
- 25 % des élèves étudient l'Auvergnat,
- 35 % le Berrichon
- 40 % le Corse.
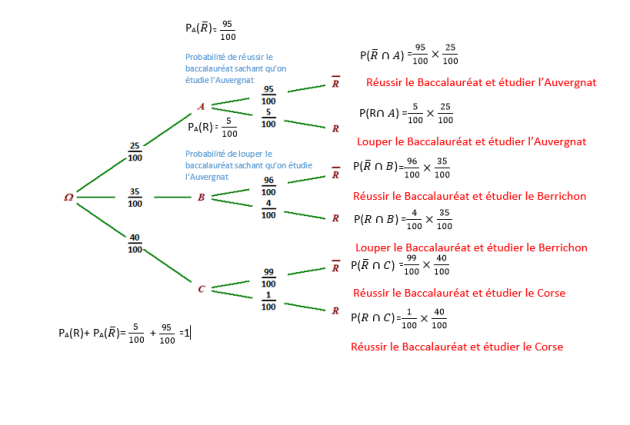
95 % des élèves qui étudient l'Auvergnat , 96 % de ceux qui étudient le Berrichon et 99 % de ceux qui étudient le Corse ont obtenus leur Bac.
On choisit un élève au hasard et on définit les événements suivants :
A : "L'élève étudie l'Auvergnat" ;
B : "L'élève étudie le Berrichon" ;
C : "L'élève étudie le Corse" ;
R : "L'élève est refusé à l'examen du Baccalauréat".
Question
1. Traduire les données de l'énoncé en utilisant les notations des probabilités.
Solution
\(p(A)=\frac{25}{100}\)
\(p(B)=\frac{35}{100}\)
\(p(C)=\frac{40}{100}\)
\(p_A(\overline{R})=\frac{95}{100}\)
\(p_B(\overline{R})=\frac{96}{100}\)
\(p_C(\overline{R})=\frac{99}{100}\)
2. Exprimer en fonction des événements A, B, C et R :
Question
a. la probabilité qu'un élève étudie le Berrichon et soit bachelier.
Solution
\(p(B \cap \overline{R})\)
Calcul de cette valeur :
\(p_B(\overline{R})=\frac{p(\overline{R} \cap B)}{p(B)}\)
\(\iff p(\overline{R} \cap B)= p_B(\overline{R}) \times p(B)\)
\(\iff p(\overline{R} \cap B)=\frac{96}{100} \times \frac{35}{100}\)
\(\iff p(\overline{R} \cap B)=\frac{24}{25} \times \frac{7}{20}\)
\(\iff p(\overline{R} \cap B)=\frac{6}{25} \times \frac{7}{5}\)
\(\iff p(\overline{R} \cap B)=\frac{42}{125}\)
Question
b. la probabilité qu'un élève étudie l'Auvergnat sachant qu'il n'a pas eu son Bac.
Solution
\(p_{R}(A)\)
Calcul de cette valeur :
\(p_{R}(A)=\frac{p(R \cap A)}{p(R)}\)
\(p_A(\overline{R})=\frac{p(\overline{R} \cap A )}{p(A)}\)
\(\iff p(\overline{R} \cap A)= p_A(\overline{R}) \times p(A)\)
\(p_B(\overline{R})=\frac{p(\overline{R} \cap B )}{p(B)}\)
\(\iff p(\overline{R} \cap B)= p_B(\overline{R}) \times p(B)\)
\(p_C(\overline{R})=\frac{p(\overline{R} \cap C)}{p(C)}\)
\(\iff p(\overline{R} \cap C)= p_C(\overline{R}) \times p(C)\)
\(p(\overline{R})=p( \overline{R} \cap A)+p(\overline{R} \cap B)+p(\overline{R} \cap C)\)
\(\iff p(\overline{R})=p_A(\overline{R}) \times p(A)+p_B(\overline{R}) \times p(B)+p_C(\overline{R}) \times p(C)\)
\(\iff p(\overline{R})=\frac{95}{100} \times \frac{25}{100}+\frac{96}{100} \times \frac{35}{100}+\frac{99}{100} \times \frac{40}{100}\)
\(\iff p(\overline{R})=\frac{19}{20} \times \frac{1}{4}+\frac{24}{25} \times \frac{7}{20}+\frac{99}{100} \times \frac{2}{5}\)
\(\iff p(\overline{R})=\frac{19}{80}+\frac{6}{25} \times \frac{7}{5}+\frac{99}{50} \times \frac{1}{5}\)
\(\iff p(\overline{R})=\frac{19}{80}+\frac{42}{125} +\frac{99}{250}\)
\(\iff p(\overline{R})=\frac{19}{80}+\frac{84}{250} +\frac{99}{250}\)
\(\iff p(R)=\frac{19}{80}+\frac{183}{250}\)
\(\iff p(\overline{R})=\frac{475}{2000}+\frac{1464}{2000}\)
\(\iff p(\overline{R})=\frac{1939}{2000}\)
\(\iff p(R)=1-p(\overline{R})=1-\frac{1939}{2000}=\frac{2000}{2000}-\frac{1939}{2000}=\frac{61}{2000}\)
\(p_{R}(A)=\frac{p(R \cap A)}{p(R)}\)
\(\iff p_{R}(A)=\frac{p(R \cap A)}{\frac{61}{2000}}\)
\(p(R \cap A)=p(A) \times p_{A}(R)\)
\(\iff p(R \cap A)=\frac{25}{100} \times \frac{5}{100}\)
\(\iff p(R \cap A)=\frac{1}{4} \times \frac{1}{20}=\frac{1}{80}\)
\(\iff p_{R}(A)=\frac{\frac{1}{80}}{\frac{61}{2000}}\)
\(\iff p_{R}(A)=\frac{1}{80} \times \frac{2000}{61}\)
\(\iff p_{R}(A)=\frac{1}{8} \times \frac{200}{61}\)
\(\iff p_{R}(A)=\frac{1}{2} \times \frac{50}{61}\)
\(\iff p_{R}(A)=\frac{50}{122}\)