Exercice : Exemple 15
On considère trois urnes qui contiennent chacune des boules noires et rouges.
Une expérience consiste à tirer au hasard une boule de chaque urne.
On considère les évènements suivants
\(N_i\) : “on tire une boule noire de l'urne Ui” ;
\(R_i\) : “on tire une boule rouge de l'urne Ui”.
On considère l'arbre de probabilité suivant :
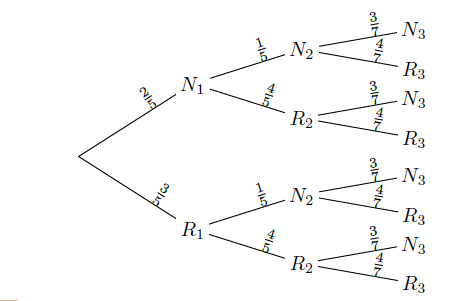
Question
1. Déterminer la probabilité de l'évènement \(N_3\).
Solution
\(p(N_3)=\frac{2}{5} \times \frac{1}{5} \times \frac{3}{7}+\frac{2}{5} \times \frac{4}{5} \times \frac{3}{7}+\frac{3}{5} \times \frac{1}{5} \times \frac{3}{7}+\frac{3}{5} \times \frac{4}{5} \times \frac{3}{7}\)
\(p(N_3)=\frac{2}{5} \times \frac{3}{7} (\frac{1}{5}+\frac{4}{5})+\frac{3}{5} \times \frac{3}{7} (\frac{1}{5} + \frac{4}{5})\)
\(p(N_3)=\frac{2}{5} \times \frac{3}{7}+\frac{3}{5} \times \frac{3}{7}\)
\(p(N_3)=(\frac{2}{5}+\frac{3}{5}) \times \frac{3}{7}\)
\(p(N_3)= \frac{3}{7}\)
Question
2. Les événements \(N_1\) et \(N_3\) sont-ils indépendants ?\(\)
Solution
\(p(N_1)=\frac{2}{5}\)
\(p(N_1 \cap N_3)=\frac{2}{5} \times \frac{1}{5} \times \frac{3}{7}+\frac{2}{5} \times \frac{4}{5} \times \frac{3}{7}\) Il y a deux chemins correspondants
\(p(N_1 \cap N_3)=\frac{2}{5} \times \frac{3}{7} (\frac{1}{5}+\frac{4}{5})=\frac{2}{5} \times \frac{3}{7}\)
donc \(p(N_1 \cap N_3)=p(N_1) \times p( N_3)\)
et les évènements \(N_1\) et \(N_3\) sont donc indépendants.