Exercice : Exemple 4
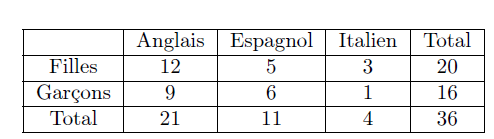
Dans une classe où les élèves étudient une seule langue vivante étrangère, certains étudient l'anglais, d'autres l'espagnol et le reste l'italien.
Question
1. On choisit un élève au hasard. Quelle est la probabilité pour que l'élève choisi étudie l'espagnol ?
On note E l'événement "L'élève choisi étudie l'espagnol"
Solution
Probabilité pour que l'élève choisi étudie l'espagnol : \(p(E)=\frac{11}{36}\)
Question
2. On choisit une fille au hasard. Quelle est la probabilité pour que la fille choisie étudie l'espagnol ?
On note \(p_F(E)\) cette probabilité
Solution
Probabilité pour que la fille choisie étudie l'espagnol \(p_F(E)=\frac{5}{20}=\frac{1}{4}\)
Question
3. On choisit au hasard un élève qui étudie l'espagnol. Quelle est la probabilité pour que l'élève choisi soit une fille ?
On note \(p_E(F) \)cette probabilité
Solution
On choisit au hasard un élève qui étudie l'espagnol.
Probabilité pour que l'élève choisi soit une fille : \(p_E(F)=\frac{5}{11}\)
Question
4. On choisit un élève au hasard et on définit les événements suivants :
A : " l'élève choisi étudie l'anglais " et G : " l'élève choisi est un garçon ".
Définir l'événement A ∩ G à l'aide d'une phrase, puis calculer P(A), P(G) et P(A ∩ G).
Solution
L'événement A ∩ G est l’événement "l'élève est un garçon et il étudie l'anglais"
\(P(A)=\frac{21}{36}=\frac{7}{12}\)
\(P(G)=\frac{16}{36}=\frac{4}{9}\)
\(P(A ∩ G)=\frac{9}{36}=\frac{1}{4}\)
Question
5. On choisit un garçon au hasard. Calculer la probabilité de l'événement " le garçon choisi étudie l'anglais ".
On note \(p_G(A) \)cette probabilité
Montrer que
\(\color{red}{p_G(A)= \frac{p(A \cap G)}{p(G)}}\)
Solution
Probabilité de l'événement " le garçon choisi étudie l'anglais " \(p_G(A))=\frac{9}{16}\)
\(\frac{p(A \cap G)}{p(G)}=\frac{\frac{1}{4}}{\frac{4}{9}}=\frac{1}{4}\times \frac{9}{4}=\frac{9}{16}\)
donc \(\color{red}{p_G(A)= \frac{p(A \cap G)}{p(G)}}\)