Exercice : Cercle trigonométrique 1
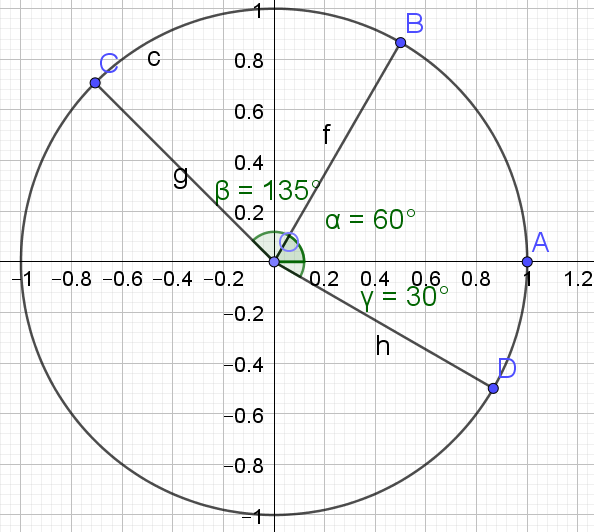
Sur un cercle trigonométrique de centre O, les points A, B, C et D sont les images respectives des réels
0 ; \(\frac{\pi}{3}\) ; \(\frac{3\pi}{4}\); \(- \frac{\pi}{6}\)
Question
1. Placer les points A, B, C et D sur le cercle .
2. Donner une mesure en radian de chaque angle :
Question
a.\( (\vec{OA} ;\vec{OB} )\)
Solution
\((\vec{OA} ;\vec{OB} )=\frac{\pi}{3}\)
Question
b. \((\vec{OC} ;\vec{OD} )\)
Solution
\((\vec{OC} ;\vec{OD})=-\frac{3\pi}{4}- \frac{\pi}{6}\)
\(\iff (\vec{OC} ;\vec{OD})=-\frac{9\pi}{12}- \frac{2\pi}{12}\)
\(\iff (\vec{OC} ;\vec{OD})=-\frac{11\pi}{12}\)
Question
c. \((\vec{OB} ; \vec{OD})\)
Solution
\((\vec{OB} ; \vec{OD})=-\frac{\pi}{3}- \frac{\pi}{6}\)
\(\iff (\vec{OB} ; \vec{OD})=-\frac{2\pi}{6}- \frac{\pi}{6}\)
\(\iff (\vec{OB} ; \vec{OD})=-\frac{3\pi}{6}\)
\(\iff (\vec{OB} ; \vec{OD})=-\frac{\pi}{2}\)
Question
d. \(( \vec{BO};\vec{DO} )\)
Solution
\(( \vec{BO};\vec{DO} )=-( \vec{OB};\vec{OD})=\frac{\pi}{2}\)
3. Donner les sinus et cosinus de :
Question
\((\vec{OA} ;\vec{OB} )\)
Solution
\(sin(\vec{OA} ;\vec{OB} )=sin(\frac{\pi}{3})\)
\(\iff sin(\vec{OA} ;\vec{OB} )=\frac{\sqrt{3}}{2}\)
\(cos(\vec{OA} ;\vec{OB} )=cos(\frac{\pi}{3})\)
\(\iff cos(\vec{OA} ;\vec{OB} )=\frac{1}{2}\)
Question
\((\vec{OB} ; \vec{OD} )\)
Solution
\(sin(\vec{OB} ;\vec{OD} )=sin(-\frac{\pi}{2})\)
\(\iff sin(\vec{OB} ;\vec{OD} )=-1\)
\(cos(\vec{OB} ;\vec{OD} )=cos(-\frac{\pi}{2})\)
\(\iff cos(\vec{OB} ;\vec{OD} )=0\)