Exercice : Cercle Trigonométrique 5
On considère les nombres réels
\(a=\frac{\pi}{6}\)
\(b=- \frac{\pi}{2}\)
\(c= \frac{3\pi}{4}\)
et \(d= \frac{\pi}{2}\).
On note A , B , C et D les images respectives des nombres a , b , c , et d sur le cercle trigonométrique de centre O représenté ci-dessous :
Question
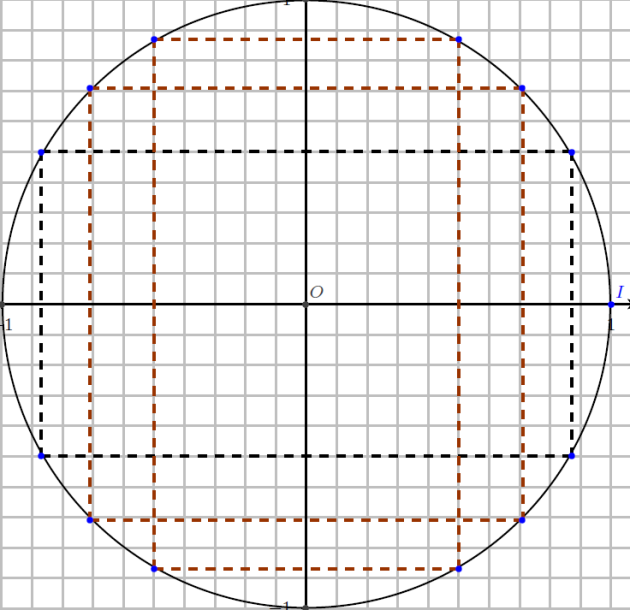
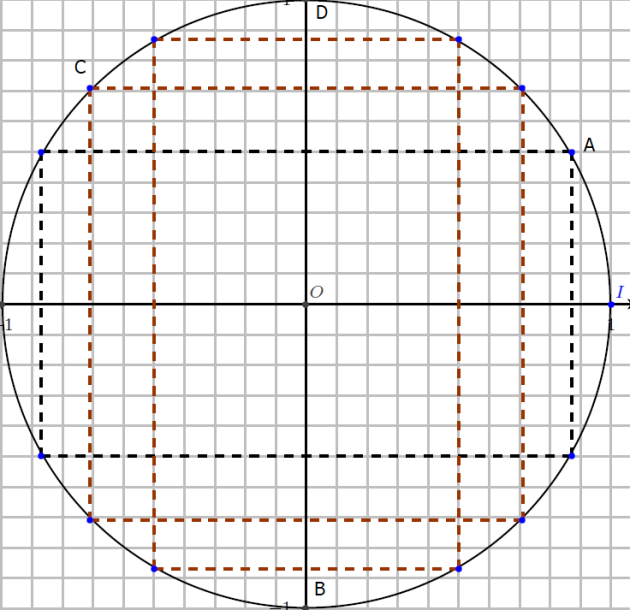
1. Placer les points A , B , C et D sur le cercle.
Question
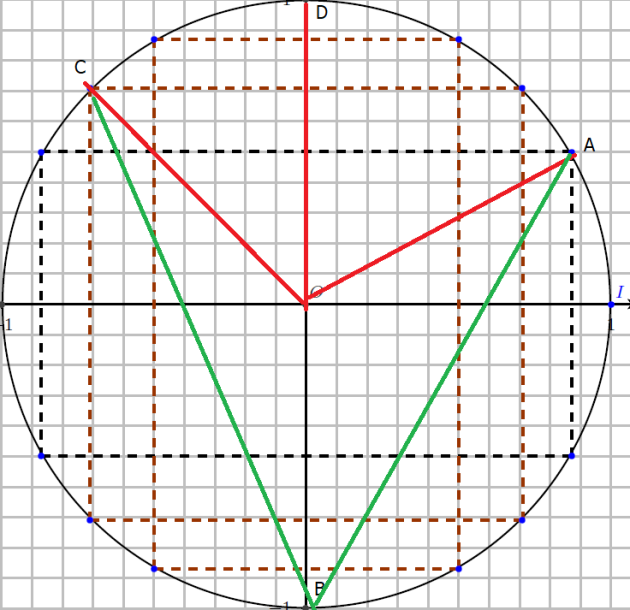
2. Déterminer les mesures respectives, en degrés, des angles \(\widehat{AOD}\) et \(\widehat{DOC}\) .
Solution
\(\widehat{AOD}=\frac{\pi}{2}-\frac{\pi}{6}=\frac{3\pi}{6}-\frac{\pi}{6}=\frac{2\pi}{6}=\frac{\pi}{3}\)
\(\widehat{DOC}=\frac{3\pi}{4}-\frac{\pi}{2}=\frac{3\pi}{4}-\frac{2\pi}{4}=\frac{\pi}{4}\)
\(\widehat{AOC}=\widehat{AOD}+\widehat{DOC}=\frac{4\pi}{12}+\frac{3\pi}{12}=\frac{7\pi}{12}\)
Question
3. En déduire la mesure en degrés de l'angle \(\widehat{ABC}\)
Solution
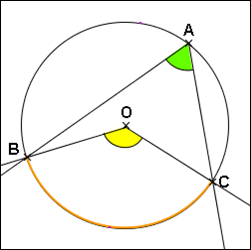
\(\color{red}{\text{Dans un cercle, si un angle inscrit et un angle au centre interceptent le même arc,}}\)
\(\color{red}{\text{alors la mesure de l'angle au centre est le double de celle de l'angle inscrit.}}\)
\(\widehat{ABC}=\frac{1}{2}\widehat{AOC}=\frac{1}{2} \times \frac{7\pi}{12}=\frac{7\pi}{24}\)
