Exercice : Cercle trigonométrique 4
Question
1.Relier chaque nombre de la colonne de gauche au seul nombre de la colonne de droite qui donne le même point du cercle trigonométrique par enroulement de la droite numérique :
\(\frac{13\pi}{3}\) | \(\frac{-3\pi}{4}\) |
\(\frac{21\pi}{4}\) | 0 |
\(\frac{-11\pi}{6}\)\(\) | \(\frac{\pi}{6}\) |
\(\frac{27\pi}{2}\) | \(\frac{-2\pi}{3}\) |
\(14\pi\) | \(\frac{-\pi}{2}\) |
\(\frac{10\pi}{3}\) | \(\frac{\pi}{3}\) |
Solution
\(14\pi = 7 \times 2\pi \mapsto 0\)
\(\frac{27\pi}{2}-\frac{-\pi}{2}=\frac{27\pi}{2}+\frac{\pi}{2}=\frac{28\pi}{2}=14 \pi =7 \times 2\pi\)
\(\frac{13\pi}{3}-\frac{\pi}{3}=\frac{12\pi}{3}=4\pi =2 \times 2\pi\)
\(\frac{21\pi}{4}-\frac{-3\pi}{4}=\frac{21\pi}{4}+\frac{3\pi}{4}=\frac{24\pi}{4}=6\pi =3 \times 2\pi\)
\(\frac{-11\pi}{6}-\frac{\pi}{6}=\frac{-12\pi}{6}=-2\pi =-1 \times 2\pi\)
\(\frac{10\pi}{3}-\frac{-2\pi}{3}=\frac{10\pi}{3}+\frac{2\pi}{3}=\frac{12\pi}{3}=4\pi=2\times 2\pi\)
\(\frac{13\pi}{3}\) | \(\frac{\pi}{3}\) |
\(\frac{21\pi}{4}\) | \(\frac{-3\pi}{4}\) |
\(\frac{-11\pi}{6}\)\(\) | \(\frac{\pi}{6}\) |
\(\frac{27\pi}{2}\) | \(\frac{-\pi}{2}\) |
\(14\pi\) | \(0\) |
\(\frac{10\pi}{3}\) | \(\frac{-2\pi}{3}\) |
Question
2. En déduire cos \(\frac{-11\pi}{6}\) et sin \(\frac{27\pi}{2}\)
Solution
\(cos \frac{-11\pi}{6} =cos \frac{\pi}{6}=\frac{\sqrt{3}}{2}\)
\(sin \frac{27\pi}{2}=sin \frac{-\pi}{2}=-1\)
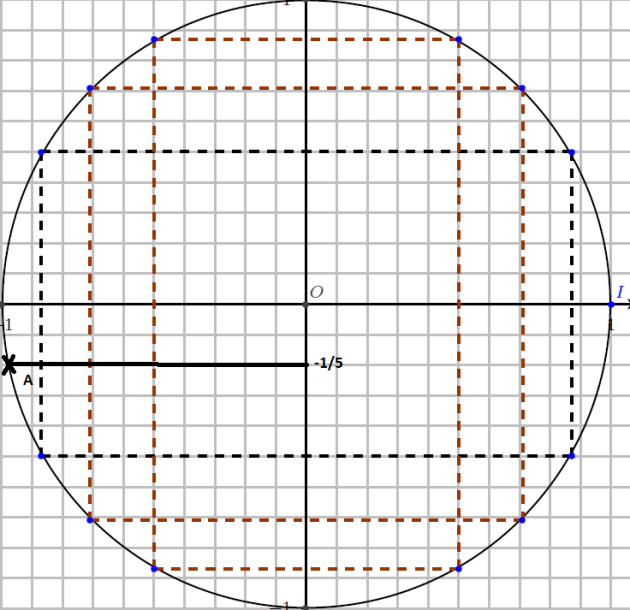
\(a\) désigne un nombre réel de l'intervalle \([\frac{\pi}{2} ; \frac{3\pi}{2}]\) tel que \(sin a =\frac{-1}{5}\)
Question
a. Placer le point A associé au réel \(a\) sur le cercle trigonométrique.
Question
b. Calculer la valeur exacte de \(cos a\).
Solution
\(cos^2a+sin^2a=1\)
\(\iff cos^2a+(\frac{-1}{5})^2=1\)
\(\iff cos^2a+\frac{1}{25}=1\)
\(\iff cos^2a=1-\frac{1}{25}\)
\(\iff cos^2a=\frac{25}{25}-\frac{1}{25}\)
\(\iff cos^2a=\frac{24}{25}\)
\(\iff cos a=-\sqrt{\frac{24}{25}}\) ou \(cos a=\sqrt{\frac{24}{25}}\)
or \(a \in [\frac{\pi}{2} ; \frac{3\pi}{2}]\) donc \(cos a<0\)
On en déduit que \(cos a=-\sqrt{\frac{24}{25}}=-\frac{\sqrt{24}}{5}\)
\(\iff cos a=-\frac{\sqrt{4\times 6}}{5}\)
\(\iff cos a=-\frac{2\sqrt{6}}{5}\)