Exercice : Cercle Trigonométrique 8
Calculer le cosinus et le sinus des réels :
Question
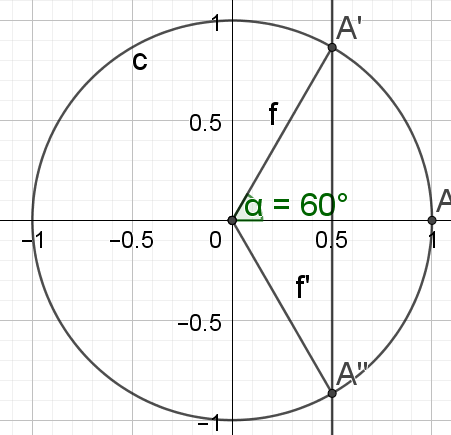
\(\frac{7\pi}{6}\)
Solution
\(cos \frac{7\pi}{6}=cos (\frac{6\pi}{6}+\frac{\pi}{6})=cos (\pi+\frac{\pi}{6})=-cos (\frac{\pi}{6})=-\frac{\sqrt{3}}{2}\)
\(sin \frac{7\pi}{6}=sin(\frac{6\pi}{6}+\frac{\pi}{6})=sin (\pi+\frac{\pi}{6})=-sin(\frac{\pi}{6})=-\frac{1}{2}\)
Question
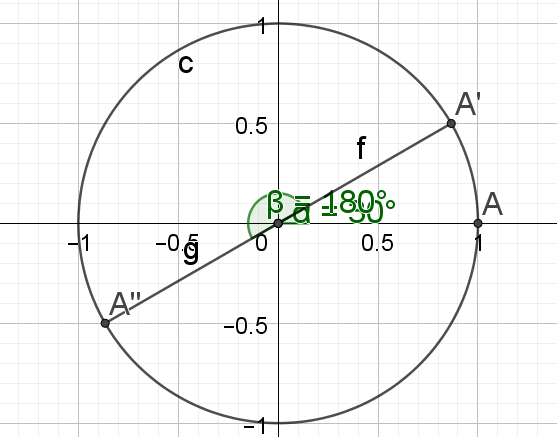
\(\frac{-7\pi}{3}\)
Solution
\(cos \frac{-7\pi}{3}=cos (\frac{-6\pi}{3}+\frac{-\pi}{3})=cos (-2\pi+\frac{-\pi}{3})=cos (\frac{-\pi}{3})=cos (\frac{\pi}{3})=\frac{1}{2}\)
\(sin \frac{-7\pi}{3}=sin(\frac{-6\pi}{3}+\frac{-\pi}{3})=sin (-2\pi+\frac{-\pi}{3})=sin(\frac{-\pi}{3})=-sin(\frac{\pi}{3})=-\frac{\sqrt{3}}{2}\)
Question
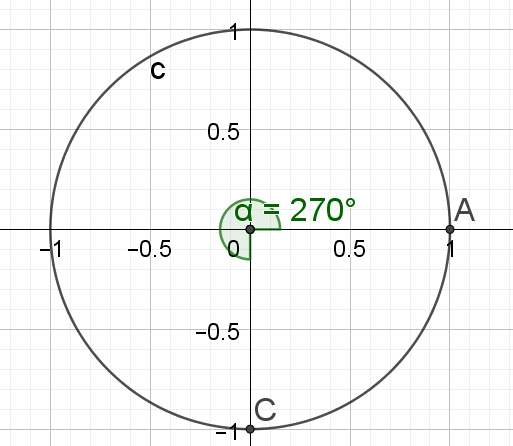
\(\frac{3\pi}{2}\)
Solution
\(cos \frac{3\pi}{2}=0\)
\(sin \frac{3\pi}{2}=-1\)