Exercice : Cercle trigonométrique 2
Dans le plan muni d'un repère orthonormé \((O;\vec{i};\vec{j})\), on donne le point A(1; 0).
Question
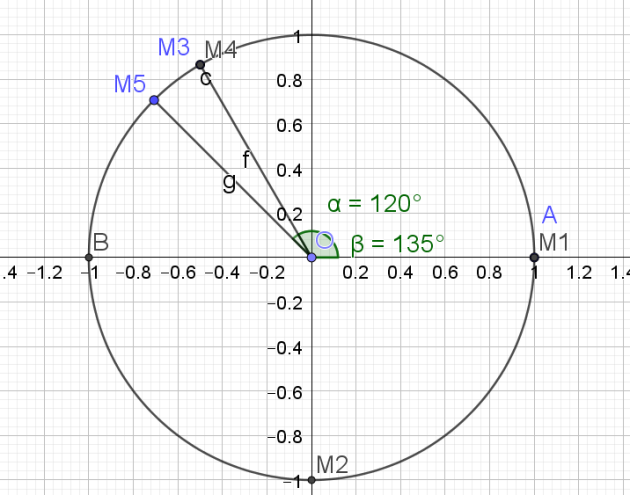
1.Représenter les points \(M_1, M_2,...,M_5\) du cercle trigonométrique tels que
les angles \((\vec{OA};\vec{OM_i})\) aient comme mesures respectives :
\(6\pi ;\frac{-9\pi}{2};\frac{2\pi}{3};\frac{-7\pi}{6};\frac{3\pi}{4}\)
Question
b. Déterminer la mesure principale de chacun de ces angles orientés de vecteurs.
Solution
\(6\pi \mapsto 0\)
\(\frac{-9\pi}{2} \mapsto \frac{-\pi}{2}\)
\(\frac{2\pi}{3} \mapsto \frac{2\pi}{3}\)
\(\frac{-7\pi}{6} \mapsto \frac{-7\pi}{6}+2\pi=\frac{-7\pi}{6}+\frac{12\pi}{6}=\frac{5\pi}{6}\)
\(\frac{3\pi}{4} \mapsto \frac{3\pi}{4}\)
Question
c. Déterminer : \(cos(\vec{OA};\vec{OM_1})\)
Solution
\(cos(\vec{OA};\vec{OM_1})=cos 0=1\)
Question
\(sin(\vec{OA};\vec{OM_3})\)
Solution
\(sin(\vec{OA};\vec{OM_3})=sin(\frac{2\pi}{3})=sin(\frac{\pi}{3})=\frac{\sqrt{3}}{2}\)
Question
\(cos(\vec{OM_2};\vec{OM_5})\)
Solution
\(cos(\vec{OM_2};\vec{OM_5})=cos(-\frac{3\pi}{4})=-\frac{\sqrt{2}}{2}\)
Question
\(sin(3\vec{i};2\vec{j})\)
Solution
\(sin(3\vec{i};2\vec{j})=sin(\frac{\pi}{2})=1\)
Question
\(cos(\vec{i};-\vec{i}-\vec{j})\)
Solution
\(cos(\vec{i};-\vec{i}-\vec{j})=cos(\frac{-\pi}{2})=0\)