Exercice : Cercle Trigonométrique 7
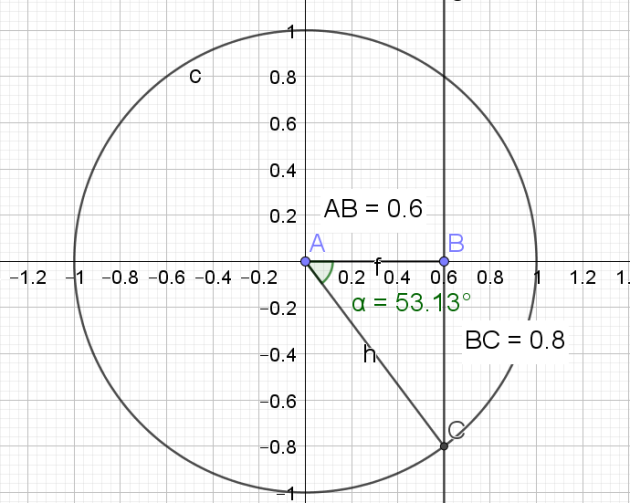
Question
Sachant que \(cos x = 0,6\) et que \(x \in [- \frac{\pi}{2} ; 0 ]\) , déterminer \(sin(x)\) et \(cos (- x)\).
Solution
\(cos^2(x)+sin^2(x)=1\)
\(0,6^2+sin^2(x)=1\)
\(0,36+sin^2(x)=1\)
\(sin^2(x)=1-0,36\)
\(sin^2(x)=0,64\)
\(sin(x)=0,8\) ou \(sin(x)=-0,8\)
mais \(x \in [- \frac{\pi}{2} ; 0 ]\) donc \(sin(x)<0\) et donc \(sin(x)=-0,8\)
\(cos (- x)=cos(x)\) donc \(cos (- x)\)=0,6
Question
Sachant que \(sin x = - \frac{\sqrt{2}}{5}\) et que\( x \in [ - \pi ; - \frac{\pi}{2} ]\), déterminer \(cos x\)
Solution
\(cos^2(x)+sin^2(x)=1\)
\(cos^2(x)+(- \frac{\sqrt{2}}{5})^2=1\)
\(cos^2(x)+\frac{2}{25}=1\)
\(cos^2(x)=1-\frac{2}{25}\)
\(cos^2(x)=\frac{25}{25}-\frac{2}{25}\)
\(cos^2(x)=\frac{23}{25}\)
\(cos(x)=\sqrt{\frac{23}{25}}\)
\(cos(x)=\frac{\sqrt{23}}{5}\) ou \(cos(x)=-\frac{\sqrt{23}}{5}\)
mais \(x \in [ - \pi ; - \frac{\pi}{2} ]\) donc \(cos x\)<0
et donc finalement \(cos(x)=-\frac{\sqrt{23}}{5}\)