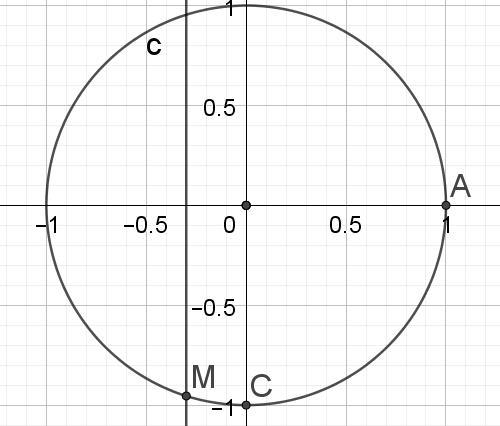
Exercice : Cercle Trigonométrique 6

On saît que \(cos(x)=-0,3\) et que \(x\in [-\pi ;\frac{-\pi}{2}]\)

Question

a.Placer le point M image de \(x\) sur le cercle C.

Solution

Question

b.Déterminer les coordonnées de M.

Solution

\(cos^2(x)+sin^2(x)=1\)

or \(cos(x)=-0,3\)

donc

\((-0,3)^2+sin^2(x)=1\)

\(\iff 0,09+sin^2(x)=1\)

\(\iff sin^2(x)=1-0,09\)

\(\iff sin^2(x)=0,91\)

\iff \(sin(x)=\sqrt{0,91}\) ou \(sin(x)=-\sqrt{0,91}\)

or \(x \in [-\pi ;-\frac{\pi}{2}[\) donc \(sin(x) <0\)

Finalement : \(sin(x)=-\sqrt{0,91}\)