Exercice : Roue Colorée et Fonction
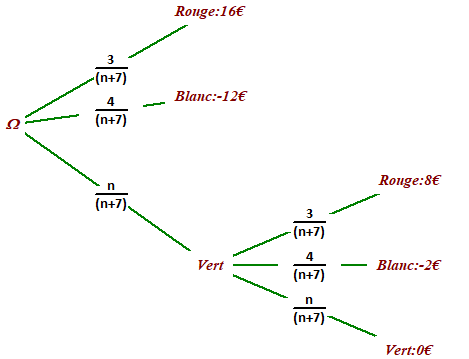
Une roue de loterie se compose de secteurs identiques : trois de ces secteurs sont rouges, quatre sont blancs et \(n\) sont verts (avec \(n≥1\)).
Un joueur fait tourner la roue devant un repère fixe ; chaque secteur a la même probabilité de s'arrêter devant ce repère.
si le secteur repéré est rouge, le joueur gagne 16 € ;
s'il est blanc, il perd 12 € ;
s'il est vert, il lance une deuxième fois la roue :
(a) si le secteur repéré est rouge, il gagne 8 € ;
(b) s'il est blanc, il perd 2 € ;
(c) s'il est vert, il ne gagne rien et ne perd rien.
On appelle \(G\) la variable aléatoire comptabilisant le gain algébrique du joueur à l'issue d'une partie.
Question
a. Déterminer la loi de probabilité de la variable aléatoire \(G\).
Solution
\(g_i\) | 16 | 8 | 0 | -2 | -12 |
|---|---|---|---|---|---|
\(p(G=g_i)\) | \(\frac{3}{n+7}\) | \(\frac{n}{n+7} \times \frac{3}{n+7}=\frac{3n}{(n+7)^2}\) | \(\frac{n}{n+7} \times \frac{n}{n+7}=\frac{n^2}{(n+7)^2}\) | \(\frac{n}{n+7} \times \frac{4}{n+7}=\frac{4n}{(n+7)^2}\) | \(\frac{4}{n+7}\) |
Question
b. Lors d'une partie, quelle est en fonction de \(n\) la probabilité d'avoir un gain positif ?
Solution
\(p(G \ge 0)=\frac{n^2}{(n+7)^2}+\frac{3n}{(n+7)^2}+\frac{3}{n+7}\)
\(\iff p(G \ge 0)=\frac{n^2}{(n+7)^2}+\frac{3n}{(n+7)^2}+\frac{3(n+7)}{(n+7)^2}\)
\(\iff p(G \ge 0)=\frac{n^2+3n+3(n+7)}{(n+7)^2}\)
\(\iff p(G \ge 0)=\frac{n^2+3n+3n+21}{(n+7)^2}\)
\(\iff p(G \ge 0)=\frac{n^2+6n+21}{(n+7)^2}\)
Question
c. Montrer que l'espérance mathématique de la variable aléatoire \(G\) est
\(E(G)=\frac{16n}{(n+7)^2}\)
Solution
\(E(G)=16×\frac{3}{n+7}+8×\frac{3n}{(n+7)2} +(−2)×\frac{4n}{(n+7)^2}+0×\frac{n^2}{(n+7)^2}+(−12)× \frac{4}{n+7}\)
\(\iff E(G)=\frac{48}{n+7}+\frac{24n}{(n+7)2} +\frac{-8n}{(n+7)^2}+\frac{-48}{n+7}\)
\(\iff E(G)=\frac{24n}{(n+7)2} +\frac{-8n}{(n+7)^2}\)
\(\iff E(G)=\frac{16n}{(n+7)^2}\)
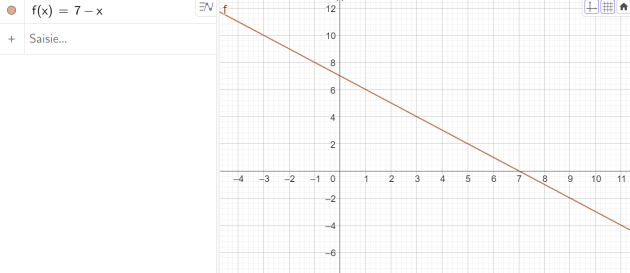
2 .On définit , sur [0;+∞[ , la fonction \(f:x↦\frac{x}{(x+7)^2}\).
Question
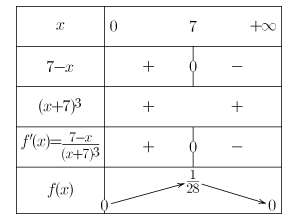
a. Étudier les variations de la fonction \(f\).
Solution
Calculons la dérivée de la fonction \(f\):
\(f′(x)=\frac{1(x+7)^2−x×2(x+7)}{(x+7)^4}=\frac{(x+7)−2x}{(x+7)^3}=\frac{7−x}{(x+7)^3}\)
Si \(x \ge 0\)
alors \(x+7 \ge 7\)
\(\iff (x+7)^3 \ge 7^3\)
\(\iff (x+7)^3 \ge 343 \ge 0\)
Etude du signe de la fonction \(x \mapsto 7-x\)
\(f(0)=\frac{0}{(0+7)^2}=0\)\(\)
\(\lim\limits_{x \to +\infty} f(x)=0\)
\(f(7)=\frac{7}{(7+7)^2}=\frac{7}{(2 \times 7)^2}=\frac{7}{4 \times 7^2}=\frac{1}{4 \times 7}=\frac{1}{28}\)
Question
b. En déduire la valeur de \(n\) pour laquelle l'espérance mathématique \(E(G)\)est maximale.
Que vaut l'espérance mathématique dans ce cas ?
Solution
Valeur deu nombre de secteur \(n\) maximisant l'espérance mathématique E(G)
\(E(G)=\frac{16n}{(n+7)^2}=16f(n)\)
donc le maximum de la fonction \(f\) correspond au maximum de la fonction \(E\).
Le maximum est donc atteint pour \(n=7\).
\(E(G)=16×\frac{1}{28}=\frac{16}{28}=\frac{4}{7}≈0,57€\)
Le joueur pourra alors espérer gagner 0,57 €