Exercice : Exemple 17 :
Une urne contient 2 boules blanches et 3 boules noires. On tire au hasard une boule et on ne la remet pas dans l'urne.
On répète cette expérience deux fois de suite.
Question
1.Ces expériences sont elles indépendantes et identiques ?
Solution
Ces expériences ne sont pas indépendantes car elles n'ont pas les même issues car la première boule tirée influe sur le nombre de boules de chaque couleur restant dans l'urne.
Ces expériences ne sont pas identiques car les probabilités ne sont pas les mêmes lors du premier et second tirage.
Question
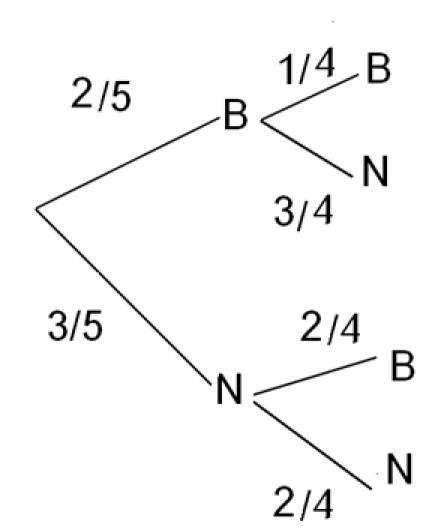
2.Représenter l'ensemble des issues de ces expériences dans un arbre.
On note B l'issue "On tire une boule blanche" et N l'issue "On tire une boule noire".
Question
3.Quelle est la probabilité d'obtenir au moins une boule blanche p(B≥1) ?
Solution
\(p(B≥1)=\frac{2}{5}+\frac{3}{5}\times \frac{2}{4}=\frac{2}{5}+\frac{6}{20}\)
\(=\frac{8}{20}+\frac{6}{20}=\frac{14}{20}\)
\(p(B≥1)=0,7\)
Question
4.Quelle est la probabilité d'obtenir au moins une boule noire p (N≥1) ?
Solution
\(p (N≥1)=\frac{3}{5}+\frac{2}{5}\times \frac{3}{4}=\frac{3}{5}+\frac{6}{20}\)
\(=\frac{8}{20}+\frac{6}{20}=\frac{14}{20}\)
\(p(N≥1)=0,7\)