Exercice : Exemple 11 :
Un sac contient les jetons numérotés ci-dessous.
On pioche au hasard un jeton du sac.
Un jeu est organisé ainsi : pour une mise de trois euros, on gagne autant qu'indiqué sur le jeton.
On définit la variable aléatoire X qui lui associe le bénéfice du joueur.
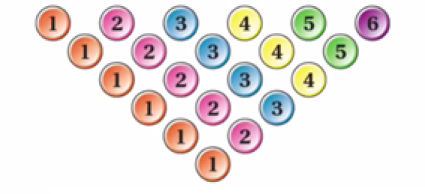
Question
1.Montrer que X prend des valeurs comprises entre -2 et 3
Solution
Comme la mise est de 3€,les gains vont de 1-3=-2€ à 6-3=3€
Question
2.Déterminer la loi de probabilité de X.
Solution
\(x_i\) | -2 | -1 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|---|---|
\(p(X=x_i)\) | \(\frac{6}{21}\) | \(\frac{5}{21}\) | \(\frac{4}{21}\) | \(\frac{3}{21}\) | \(\frac{2}{21}\) | \(\frac{1}{21}\) |
Question
3.Calculer E(X) et interpréter ce résultat.
Solution
\(E(X)=\frac{1}{21}(6×(-2)+5×(-1)+⋯+3×1)=\frac{-7}{21}=\frac{-1}{3}\simeq-0,33\)
donc \(\color{red}{\textbf{ Le jeu n'est pas intéressant pour le joueur car }}\)
\(\color{red}{\textbf{on peut "espérer" une moyenne des gains négative sur un grand nombre de parties.}}\)
Question
4.Calculer V(X) et \(\sigma(X)\) interpréter ces résultats.
Solution
\(V(X)=\frac{1}{21}(6×(-2-\frac{-1}{3})^2+5×(-1-\frac{-1}{3})^2+4×(0-\frac{-1}{3})^2+3×(1-\frac{-1}{3})^2+2×(2-\frac{-1}{3})^2+1×(3-\frac{-1}{3})^2)\)
\(V(X)=\frac{1}{21}(6×(-\frac{6}{3}+\frac{1}{3})^2+5×(-\frac{3}{3}+\frac{1}{3})^2+4×(\frac{1}{3})^2+3×(\frac{3}{3}+\frac{1}{3})^2+2×(\frac{6}{3}+\frac{1}{3})^2+1×(\frac{9}{3}+\frac{1}{3})^2)\)
\(V(X)=\frac{1}{21}(6×(-\frac{5}{3})^2+5×(-\frac{2}{3})^2+4×(\frac{1}{3})^2+3×(\frac{4}{3})^2+2×(\frac{7}{3})^2+1×(\frac{10}{3})^2)\)
\(V(X)=\frac{1}{21}(6×\frac{25}{9}+5×\frac{4}{9}+4×\frac{1}{9}+3×\frac{16}{9}+2×\frac{49}{9}+1×\frac{100}{9})\)
\(V(X)=\frac{1}{21}(\frac{150}{9}+\frac{20}{9}+\frac{4}{9}+\frac{48}{9}+\frac{98}{9}+\frac{100}{9})\)
\(V(X)=\frac{1}{21}\times \frac{420}{9}\)
\(V(X)=\frac{20}{9}\simeq2,22\)
\(\sigma(X)=\sqrt{\frac{20}{9}}\)
\(\sigma(X)=\frac{\sqrt{20}}{3}\simeq1,49\)
\(\color{red}{\textbf{Le plus probable est que le gain soit compris entre } [E(X)-\sigma(X) ;E(X)+\sigma(X)]}\)
\(\color{red}{\simeq[-0,33-1,49 ;-0,33+1,49]=[-1,82 ;1,16 ]}\)
\(\color{red}{\textbf{soit entre -1,82 et 1,16€ par parties pour un grand nombre de parties}}\)