III. Variance - Ecart type d'une variable aléatoire
Définition : La variance de la loi de probabilité de la variable aléatoire \(X\)
\(\color{red}{\textbf{La variance de la loi de probabilité de X est :}}\)
\(\color{red}{V(X)= p(X=x_1)×(x_1-E(X))^2+ p(X=x_2) ×(x_2-E(X))^2 + ... + p(X=x_n) ×(x_n-E(X))^2}\)
\(\color{red}{V(X)=\sum_{i=1}^n p_i \times (x_i-E(X))^2=E(X^2)-E^2(X)}\)
Complément : Démonstration
\(V(X)=\sum_{i=1}^n p_i \times (x_i-E(X))^2\)
\(\iff V(X)=\sum_{i=1}^n p_i \times (x_i^2-2x_iE(X)+E^2(X))\)
\(\iff V(X)=\sum_{i=1}^n p_i \times x_i^2-2(\sum_{i=1}^n p_ix_iE(X))+\sum_{i=1}^n p_iE^2(X)\)
\(\iff V(X)=E(X^2)-2(\sum_{i=1}^n p_ix_i)E(X)+(\sum_{i=1}^n p_i)E^2(X)\)
\(\iff V(X)=E(X^2)-2E(X) \times E(X)+E^2(X)\) car \(\sum_{i=1}^n p_i=1\)
\(\iff V(X)=E(X^2)-2E(X) \times E(X)+E^2(X)\)
\(\iff V(X)=E(X^2)-2E(X)^2+E^2(X)\)
\(\iff V(X)=E(X^2)-E^2(X)\)
Définition : L‘écart type de la loi de probabilité de la variable aléatoire \(X\)
\(\color{red}{\textbf{L‘écart type de la loi de probabilité de X est :} \sigma(X) = \sqrt{V(X)}}\)
Remarque :
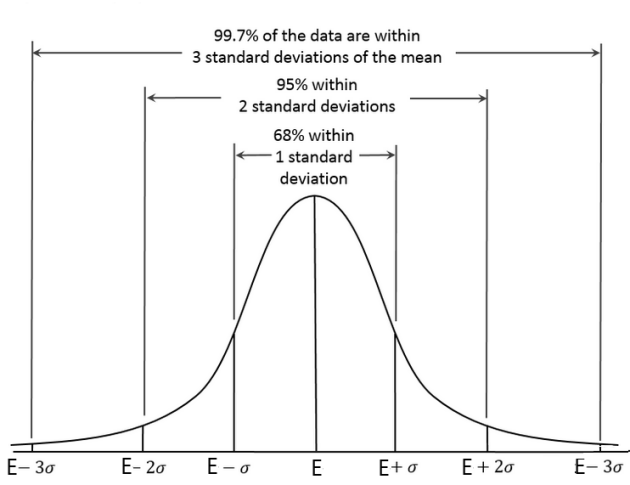
\(\color{red}{\textbf{La plupart des résultats de l'expérience seront situés dans l'intervalle} [E(X)-\sigma(X) ;E(X)+\sigma(X)]}\)
Remarque :
\(\color{red}{\textbf{La variance et l'écart type d'une variable aléatoire ont }}\)
\(\color{red}{\textbf{les mêmes définitions que la variance et l'écart type d'une série statistique.}}\)
Fondamental : Propriétés
\(\color{red}{\textbf{Soit une variable aléatoire X définie sur un univers } \Omega.}\)
\(\color{red}{\textbf{Soit a et b deux nombres réels.}}\)
\(\color{red}{\textbf{On a : }}\)
\(\color{red}{\begin{cases}E(aX+b) = aE(X)+b\\V(aX+b) = a^2V(X)\end{cases}}\)
Remarque :
La variance et l‘écart type mesurent la dispersion des valeurs de la variable aléatoire X autour de l’espérance.
Complément : Démonstration
\(E(aX+b)=\sum_{i=1}^n p_i(ax_i+b)\)
\(=a\sum_{i=1}^n p_ix_i+b\sum_{i=1}^n p_i\)
\(=a\sum_{i=1}^n p_ix_i+b\)
\(=aE(X)+b\)
\(V(aX+b)=\sum_{i=1}^n p_i(ax_i+b-(E(aX+b)))^2\)
\(=\sum_{i=1}^n p_i(ax_i+b-(aE(X)+b))^2\)
\(=a^2\sum_{i=1}^n p_i(x_i-E(X))^2\)
\(=a^2V(X)\)