Exercice : Exemple 6 :
On lance un dé équilibré à 6 faces:
si la face supérieure est 1,2 ou 3, on perd 6€ ;
si la face supérieure est 4 ou 5,on gagne 2€,
sinon on gagne 8€
Question
1. Calculer le gain moyen que peut espérer un joueur
Solution
Face | 1,2,3 | 4,5 | 6 |
|---|---|---|---|
Gain | -6 | 2 | 8 |
\(\color{red}{\textbf{On peut donc définir une fonction X qui a chaque issue associe le gain.}}\)
\(\begin{cases}p(X=-6)=\frac{3}{6}=\frac{1}{2}\\p(X=2)=\frac{2}{6}=\frac{1}{3}\\p(X=8)=\frac{1}{6}\end{cases}\)
\(x_i\) | -6 | 2 | 8 |
|---|---|---|---|
\(p(X =x_i)\) | \(\frac{1}{2}\) | \(\frac{1}{3}\) | \(\frac{1}{6}\) |
Ce tableau résume la \(\color{red}{\underline{\textbf{Loi de probabilité}}}\) de la \(\color{red}{\underline{\textbf{variable aléatoire X}}}\).
\(\frac{1}{2} \times (-6)+\frac{1}{3} \times 2 +\frac{1}{6} \times 8\)
\(=\frac{-6}{2}+\frac{2}{3}+\frac{8}{6}\)
\(=\frac{-18}{6}+\frac{4}{6}+\frac{8}{6}\)
\(=\frac{-6}{6}=-1<0\)
donc \(\color{red}{\textbf{Sur un grand nombre de parties on peut "espérer" que le joueur perd 1€.Ce jeu est donc en défaveur du joueur}}\)
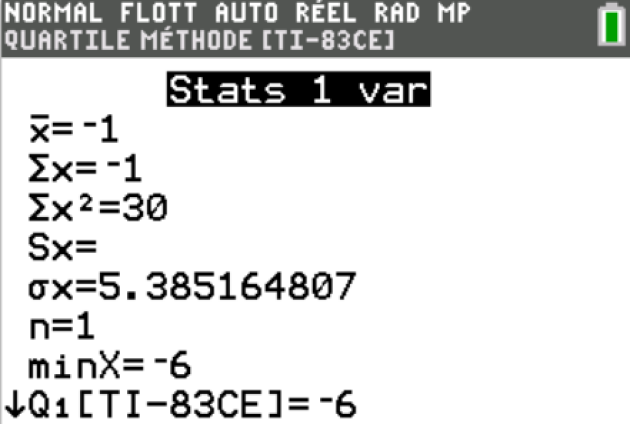
Question
2. Utiliser la calculatrice pour retrouver ce résultat.