Exercice : Exemple 10 :
Une urne contient trois boules blanches et une boule noire.
On tire au hasard les boules dans l'urne, une par une, jusqu'à obtenir la boule noire.
Question
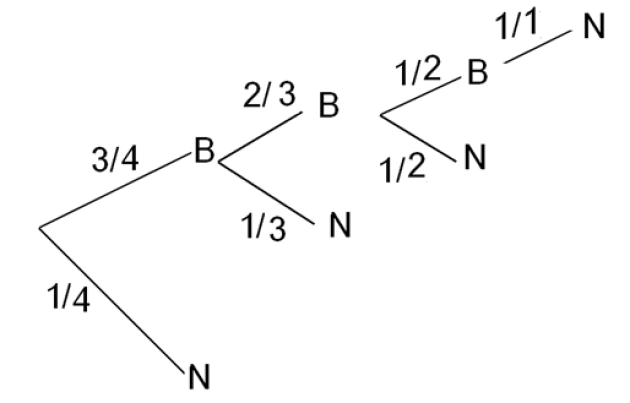
1. Construire un arbre permettant de calculer la probabilité d'avoir la boule noire au premier, au second, au troisième et au dernier tirage.
Question
2. Soit R la variable aléatoire qui donne le rang de la sortie de la boule noire. Calculer E(R),V(R),\(\sigma(R)\)Interpréter ses résultats.
Solution
\(r_i\) | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
\(p(R=r_i)\) | \(\frac{1}{4}\) | \(\frac{3}{4}\times \frac{1}{3}=\frac{1}{4}\) | \(\frac{3}{4}\times \frac{2}{3}\times \frac{1}{2}=\frac{1}{4}\) | \(\frac{3}{4}\times \frac{2}{3}\times \frac{1}{2}\times \frac{1}{1}=\frac{1}{4}\) |
\(E(R)=\frac{1}{4} (1+2+3+4)=\frac{1}{4} (\frac{4\times 5}{2})=\frac{5}{2}=2,5\)
\(V(R)=\frac{1}{4}((1-2,5)^2+⋯+(4-2,5)^2)\simeq 1,25\)
\(\sigma(R)\simeq \sqrt{1,25}\simeq1,12\)
\(\color{red}{\textbf{Donc on peut espérer tirer la boule noire au bout de 2 ou 3 tirages en moyenne. (2,5 tirages)}}\)
\(\color{red}{\textbf{ pour un grand nombre de répétitions de l'expérience}}\)
\(\color{red}{\textbf{mais le plus probable est de la tirer entre} [E(R)-\sigma(R) ;E(R)+\sigma(R)]\simeq[2,5-1,12 ;2,5+1,12]=[1,38 ;3,62]}\)
\(\color{red}{\textbf{donc entre le 1er et le 4ème tirage}}\)