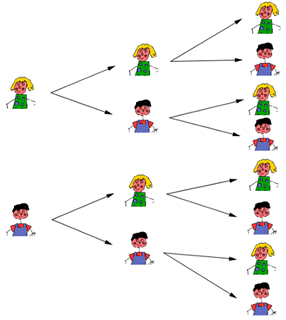
Exercice : Exemple 2 : [Chapitre XI Variables aléatoires]

Exercice : Exemple 2 :

On s'intéresse aux familles composées de trois enfants.

1. Construire un arbre regroupant toutes les issues possibles.

2. Compléter le tableau ci-dessous :

Composition possible de la famille	FFF	FFG	FGF	FGG	GFF	GFG	GGF	GGG
Nombre de filles

\(\color{red}{\textbf{On peut donc définir une fonction X qui a chaque issue associe le nombres de filles dans la famille.}}\)

\(\color{red}{\textbf{Cette fonction prend donc les valeurs 0,1,2,3}}\)

\(\begin{cases}p(X=0)=\\p(X=1)=\\p(X=2)=\\p(X=3)=\end{cases}\)

Composition possible de la famille	FFF	FFG	FGF	FGG	GFF	GFG	GGF	GGG
Nombre de filles	3	2	2	1	2	1	1	0

\(\begin{cases}p(X=0)=\frac{1}{8}\\p(X=1)=\frac{3}{8}\\p(X=2)=\frac{3}{8}\\p(X=3)=\frac{1}{8}\end{cases}\)

3. On peut résumer les résultats dans un tableau.Compléter le tableau :

\(x_i\)	0	1	2	3
\(p(X =x_i)\)

Ce tableau résume la \(\color{red}{\underline{\textbf{Loi de probabilité}}}\) de la \(\color{red}{\underline{\textbf{variable aléatoire X}}}\).

3. On peut résumer les résultats dans un tableau.Compléter le tableau :

\(x_i\)	0	1	2	3
\(p(X =x_i)\)	\(\frac{1}{8}\)	\(\frac{3}{8}\)	\(\frac{3}{8}\)	\(\frac{1}{8}\)

Ce tableau résume la \(\color{red}{\underline{\textbf{Loi de probabilité}}}\) de la \(\color{red}{\underline{\textbf{variable aléatoire X}}}\).

\(\color{red}p(X=0)+p(X=1)+p(X=2)+p(X=3)=1\)

4. Quel est le nombre moyen de filles par famille que l'on peut espérer ?

Le nombre moyen de filles par famille est donc :

\(0 \times \frac{1}{8} +1 \times \frac{3}{8} +2 \times \frac{3}{8} +3 \times \frac{1}{8}\)

=\(\frac{3}{8} + \frac{6}{8} +\frac{3}{8}\)

=\(\frac{12}{8}\)

=\(\frac{5}{4}\)

\(=1,25\)

\(\color{red}{\textbf{Le nombre moyen de filles par famille que l'on peut espérer est donc de 1 fille par famille.}}\)

\(\color{red}{\textbf{(1 est l'entier le plus proche de 1,25) }}\)