Exercice : Exemple 12 :
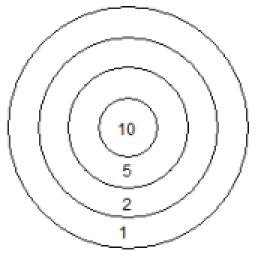
Un joueur lance des fléchettes sur une cible circulaire formée de 4 régions marquées 1, 2, 5 et 10.
Nous admettons que la probabilité que le joueur atteigne la cible est de 0,4 et que la probabilité d'atteindre la région i est inversement proportionnelle à i.
Si le joueur atteint la région i, il marque i points et 0 point s'il n'atteint pas la cible.
Soit X la variable aléatoire qui a un lancer associe le score obtenu.
Question
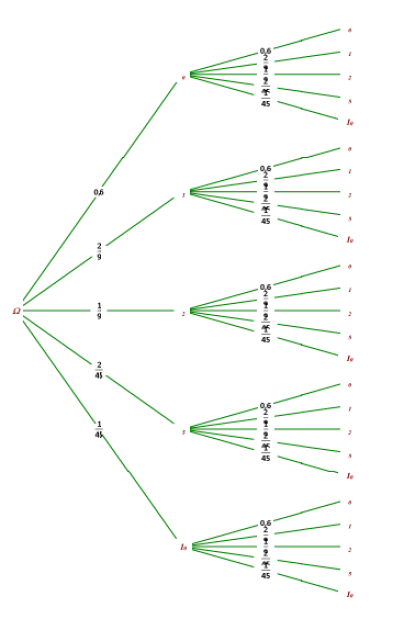
1. Donner le tableau de la loi de probabilité de la variable aléatoire X.
Solution
La probabilité d'atteindre la région i est inversement proportionnelle à i, elle est donc de la forme \(\frac{k}{i}\) où \(k\) est un réel.
On a alors :
\(0,6+\frac{k}{1}+\frac{k}{2}+\frac{k}{5}+\frac{k}{10}=1\)
soit
\(\frac{10k}{10}+\frac{5k}{10}+\frac{2k}{10}+\frac{k}{10}=0,4\)
\(\frac{18k}{10}=0,4\)
ce qui donne \(k=\frac{2}{9}\)
\(x_i\) | 0 | 1 | 2 | 5 | 10 |
|---|---|---|---|---|---|
\(p(X=x_i)\) | 0,6 | \(\frac{\frac{2}{9}}{1}=\frac{2}{9}\) | \(\frac{\frac{2}{9}}{2}=\frac{1}{9}\) | \(\frac{\frac{2}{9}}{5}=\frac{2}{45}\) | \(\frac{\frac{2}{9}}{10}=\frac{1}{45}\) |
Question
2. Combien de point un joueur peut il espérer obtenir en un lancer ?
Solution
\(E(X)=0 \times 0,6+1 \times \frac{2}{9} +2 \times \frac{1}{9} +5 \times \frac{2}{45} +10 \times \frac{1}{45}\)
\(E(X)=\frac{8}{9}\simeq0,89\)
\(\color{red}{\textbf{Donc le joueur peut espérer obtenir en moyenne sur un grand nombre de parties 0,89 point }}\)
Question
3.Quelle est la probabilité qu'il marque au moins 15 points en deux lancers ?
Solution
Il marquera au moins 15 points en deux lancers, en obtenant 5+10,10+10 ou 10+5
Les tirs étant indépendants on a :
\(p("5+10")=p("10+5")=\frac{2}{45} \times \frac{1}{45}=\frac{2}{2025}\)
\(p("10+10")=\frac{1}{45} \times \frac{1}{45}=\frac{1}{2025}\)
\(\color{red}{\textbf{donc la probabilité de marquer au moins 15 points après deux tirs est :}}\)
\(\frac{2}{2025}+\frac{2}{2025}+\frac{1}{2025}=\frac{5}{2025}=\frac{1}{405}\)