Exercice : Exemple 13 :
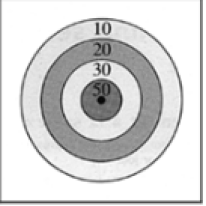
Deux tireurs X et Y s'affrontent en vue d'une sélection lors d'une épreuve comportant vingt tirs sur cible.
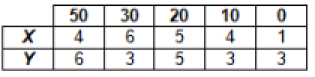
Les résultats obtenus sont les suivants.
Les nombres représentent le nombre de fléchettes tombées dans chaque case.
Question
Départager les deux tireurs en argumentant.
Solution
\(g_i\) | 50 | 30 | 20 | 10 | 0 |
|---|---|---|---|---|---|
\(p(X=x_i)\) | \(\frac{4}{20}=\frac{1}{5}\) | \(\frac{6}{20}=\frac{3}{10}\) | \(\frac{5}{20}=\frac{1}{4}\) | \(\frac{4}{20}=\frac{1}{5}\) | \(\frac{1}{20}\) |
\(p(Y=g_i)\) | \(\frac{6}{20}=\frac{3}{10}\) | \(\frac{3}{20}\) | \(\frac{5}{20}=\frac{1}{4}\) | \(\frac{3}{20}\) | \(\frac{3}{20}\) |
\(E(X)=\frac{1}{5}\times 50+ \frac{3}{10}\times 30+\frac{1}{4}\times 20+\frac{1}{5}\times 10 +\frac{1}{20}\times 0\)
\(E(X)=10+9+5+2=\fbox{26}\)
\(E(Y)=\frac{3}{10}\times 50+ \frac{3}{20}\times 30+\frac{1}{4}\times 20+\frac{3}{20}\times 10 +\frac{3}{20}\times 0\)
\(E(X)=15+4,5+5+1,5=\fbox{26}\)
\(donc \color{red}{\textbf{ L'espérance de gain est la même pour les deux joueurs.Ce paramètre ne permet pas de les départager}}\)
\(V(X)=\frac{1}{5}\times (50-26)^2+ \frac{3}{10}\times (30-26)^2+\frac{1}{4}\times (20-26)^2+\frac{1}{5}\times (10-26)^2 +\frac{1}{20}\times (0-26)^2\)
\(V(X)=\frac{1}{5}\times 24^2+ \frac{3}{10}\times 4^2+\frac{1}{4}\times 6^2+\frac{1}{5}\times 16^2 +\frac{1}{20}\times 26^2\)
\(V(X)=\frac{1}{5}\times 576+ \frac{3}{10}\times 16+\frac{1}{4}\times36+\frac{1}{5}\times 256 +\frac{1}{20}\times 676\)
\(V(X)=\frac{1152}{10}+ \frac{48}{10}+9+\frac{512}{10} +\frac{338}{10}\)
\(V(X)=\frac{1}{10}(1152+48+90+512+338)\)
\(V(X)=214\)
\(\sigma(X)=\sqrt{214}\simeq14,63\)
\([E(X)-\sigma(X),E(X)+\sigma(X)]\simeq[26-14,63 ;26+14,63]\simeq\fbox{[11,37 ;40,63]}\)
\(V(Y)=\frac{3}{10}\times (50-26)^2+ \frac{3}{20}\times (30-26)^2+\frac{1}{4}\times (20-26)^2+\frac{3}{20}\times (10-26)^2 +\frac{3}{20}\times (0-26)^2\)
\(V(Y)=\frac{3}{10}\times 24^2+ \frac{3}{20}\times 4^2+\frac{1}{4}\times 6^2+\frac{3}{20}\times 16^2 +\frac{3}{20}\times 26^2\)
\(V(Y)=\frac{3}{10}\times 576+ \frac{3}{20}\times 16+\frac{1}{4}\times 36+\frac{3}{20}\times 256 +\frac{3}{20}\times 676\)
\(V(Y)=\frac{1728}{10}+ \frac{24}{10}+9+\frac{384}{10} +\frac{338}{10}\)
\(V(Y)=\frac{1}{10}(1728+24+90+384+338)\)
\(V(Y)=256,4\)
\(\sigma(Y)=\sqrt{256,4}\simeq16\)
\([E(Y)-\sigma(Y),E(Y)+\sigma(Y)]\simeq[26-16 ;26+16]\simeq\fbox{[10 ;42]}\)
Donc
\(\color{red}{\textbf{le premier joueur a une meilleure régularité dans les lancers. car} }\)
\(\color{red}{[E(X)-\sigma(X),E(X)+\sigma(X)] \subset [E(Y)-\sigma(Y),E(Y)+\sigma(Y)] ([11,37 ;40,63] \subset[10 ;42])}\)