Exercice : Exemple 1 :
On considère le jeu suivant :
On lance un dé équilibré à 6 faces.
Si le résultat est pair, on gagne 2€.
Si le résultat est 1, on gagne 3€.
Si le résultat est 3 ou 5, on perd 4€.
Question
1.Compléter le tableau ci-dessous :
Résultat du lancer | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
Gain |
\(\color{red}{\textbf{On a défini ainsi une variable aléatoire (une fonction) X qui associe au résultat du lancer un gain en euros.}}\)
Solution
Résultat du lancer | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
Gain | 3 | 2 | -4 | 2 | -4 | 2 |
Question
2.Compléter :
\(\begin{cases}X(1)=\\X(2)=\\X(3)=\\X(4)=\\X(5)=\\X(6)=\end{cases}\)
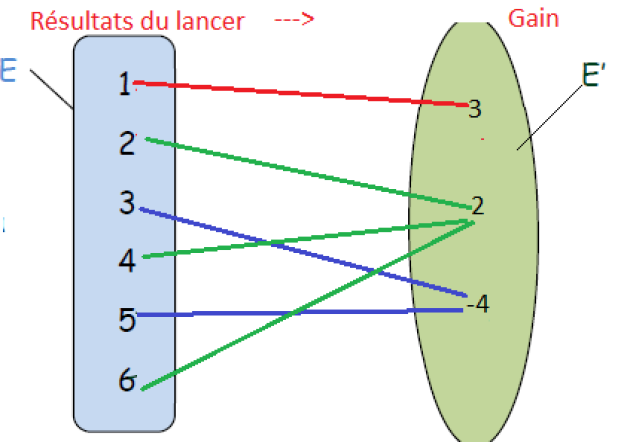
\(\color{red}{\textbf{La variable aléatoire X peut ici être considérée comme une}}\) \(\color{magenta}{fonction.}\)
qui pour des valeurs de l'ensemble E = {1 ; 2 ; 3 ; 4 ; 5 ; 6} (des faces du dé) associe des valeurs de l'ensemble {-4 ; 2 ; 3} (des gains possibles).
Solution
\(\begin{cases}X(1)=3\\X(2)=2\\X(3)=-4\\X(4)=2\\X(5)=-4\\X(6)=2\end{cases}\)
Question
3.Compléter :
\(\begin{cases}p(X=2)=\\p(X=3)=\\p(X=-4)=\end{cases}\)
Solution
\(\begin{cases}p(X=2)=\frac{3}{6}=\frac{1}{2}\\p(X=3)=\frac{1}{6}\\p(X=-4)=\frac{2}{6}=\frac{1}{3}\end{cases}\)
Question
4. On peut résumer les résultats dans un tableau Compléter le tableau :
\(x_i\) | -4 | 2 | 3 |
|---|---|---|---|
\(p(X =x_i)\) |
Ce tableau résume la \(\color{red}{\underline{\textbf{Loi de probabilité}}}\) de la \(\color{red}{\underline{\textbf{variable aléatoire X}}}\).
Solution
\(x_i\) | -4 | 2 | 3 |
|---|---|---|---|
\(p(X =x_i)\) | \(\frac{1}{3}\) | \(\frac{1}{2}\) | \(\frac{1}{6}\) |
\(\color{red}p(X=-4)+p(X=2)+p(X=3)=1\)
Question
5.Quel est le gain moyen à ce jeu ?Est il avantageux de jouer à ce jeu ?
Solution
Espérance de gains :
\(E(X)=\frac{1}{3}\times (-4)+\frac{1}{2} \times 2 +\frac{1}{6} \times 3\)
\(\iff E(X)=\frac{-4}{3}+\frac{2}{2}+\frac{3}{6}\)
\(\iff E(X)=\frac{-8}{6}+\frac{6}{6}+\frac{3}{6}\)
\(\iff E(X)=\frac{1}{6}>0\) Espérance
Donc en moyenne, on gagne \(\frac{1}{6}\) d'euro.Il est donc intéressant de jouer à ce jeu.
\(\color{red}{\textbf{Sur un grand nombre de parties le gain que peut espérer le joueur est donc positif,}}\)
\(\color{red}{\textbf{le jeu est donc favorable au joueur.}}\)
Variance des gains :
\(V(X)=\frac{1}{3}\times ((-4)-\frac{1}{6})^2+\frac{1}{2} \times (2-\frac{1}{6})^2 +\frac{1}{6} \times (3-\frac{1}{6})^2\)
\(\iff V(X)=\frac{1}{3}\times ((\frac{-24}{6}-\frac{1}{6})^2+\frac{1}{2} \times (\frac{12}{6}-\frac{1}{6})^2 +\frac{1}{6} \times (\frac{18}{6}-\frac{1}{6})^2\)
\(\iff V(X)=\frac{1}{3}\times (\frac{-25}{6})^2+\frac{1}{2} \times (\frac{11}{6})^2 +\frac{1}{6} \times (\frac{17}{6})^2\)
\(\iff V(X)=\frac{1}{3}\times \frac{625}{36}+\frac{1}{2} \times \frac{121}{36} +\frac{1}{6} \times \frac{289}{36}\)
\(\iff V(X)=\times \frac{625}{108}+ \frac{121}{72} +\frac{289}{216}\)
\(\iff V(X)=\times \frac{1250}{216}+ \frac{363}{216} +\frac{289}{216}\)
\(\iff V(X)=\times \frac{1250}{216}+ \frac{363}{216} +\frac{289}{216}\)
\(\iff V(X)=\frac{1902}{216}=\frac{317}{36}\) Variance
Ecart Type des gains :
\(\sigma(X)=\sqrt{V(X)}=\sqrt{\frac{317}{36}}\)
\(\iff \sigma(X)=\frac{\sqrt{317}}{6}\)
Intervalle des gains probables :
\([E(X)-\sigma(X) ;E(X)+\sigma(X)]=[\frac{1}{6}-\frac{\sqrt{317}}{6};\frac{1}{6}+\frac{\sqrt{317}}{6}]\)
\(\iff [E(X)-\sigma(X) ;E(X)+\sigma(X)]\simeq[-2,8;3,13]\)