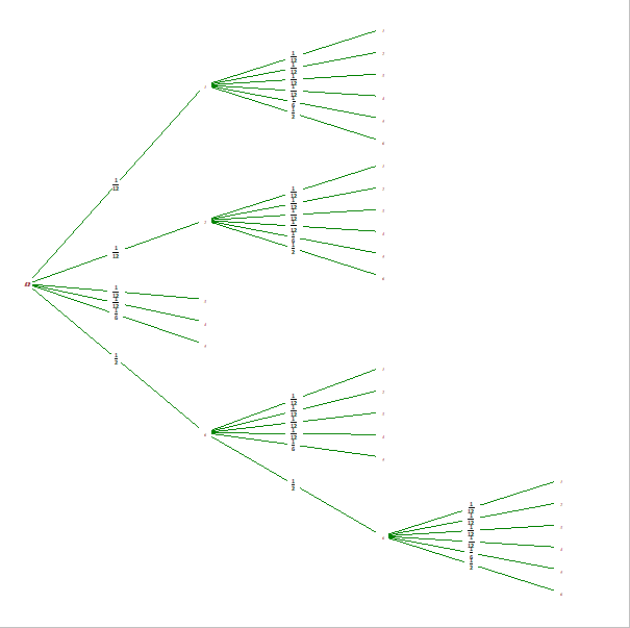
Exercice : Dé truqué
On lance un dé à 6 faces \(\color{magenta}{truqué.}\)
La probabilité d'obtenir un 1, un 2 , un 3 ou un 4 est de \(\frac{1}{12}\) pour chaque numéro.
La probabilité d'obtenir un 5 est de \(\frac{1}{6}\)
La probabilité d'obtenir un 6 est de \(\frac{1}{2}\)
Question
Question
2. Quelle est la probabilité d'obtenir deux fois un 6 en deux tirages ?
Solution
p("obtenir deux fois un 6 en deux tirages")=\(\frac{1}{2} \times \frac{1}{2}\)=\(\frac{1}{4}\)
Question
3. Quelle est la probabilité d'obtenir trois fois un 6 en trois tirages ?
Solution
p("obtenir trois fois un 6 en trois tirages")=\(\frac{1}{2} \times \frac{1}{2}\times \frac{1}{2}=\frac{1}{8}\)
Question
4. Quelle est la probabilité de ne pas obtenir de 5 ou de 6 sur deux tirages ?
Solution
p("ne pas obtenir de 5 ou de 6 sur deux tirages")=4\(\times\frac{1}{12}\times(4 \times \frac{1}{12})=\frac{16}{144}=\frac{1}{9}\)
en effet il y a 4 numéros possibles au premier tirage, les nombres de 1 à 4 et 4 numéros possibles au premier tirage, les nombres de 1 à 4.
Question
5. Quelle est la probabilité d'obtenir un seul 6 en deux tirages ?
Solution
"obtenir un seul 6 en deux tirages" :
p("Obtenir un nombre compris entre 1 et 4 puis un 6")= 4\(\times\frac{1}{12}\times \frac{1}{2}=\frac{4}{24}=\frac{1}{6}\)
p("Obtenir un nombre 5 puis un 6")= \(\frac{1}{6}\times \frac{1}{2}\)=\(\frac{1}{12}\)
p("Obtenir un nombre 6 puis un nombre différent du 6")= \(\frac{1}{2}\times(4 \times \frac{1}{12}+\frac{1}{6})=\frac{1}{2}\times( \frac{1}{3}+\frac{1}{6})\)
p("Obtenir un nombre 6 puis un nombre différent du 6")= \(\frac{1}{2}\times( \frac{2}{6}+\frac{1}{6})=\frac{1}{2}\times \frac{3}{6}=\frac{1}{2}\times \frac{1}{2}=\frac{1}{4}\)
p("obtenir un seul 6 en deux tirages")=\(\frac{1}{6}+\frac{1}{12}+\frac{1}{4}=\frac{2}{12}+\frac{1}{12}+\frac{3}{12}=\frac{6}{12}=\frac{1}{2}\)