Exercice : Avec deux dés
On lance deux dés cubiques équilibrés dont les faces sont numérotés de 1 à 6.
L'un est blanc, l'autre est noir.
On fait la somme des deux nombres obtenus et on note la somme de deux numéros indiqués par les faces supérieures des dés.
On veut déterminer la loi de probabilité des sommes possibles.
Question
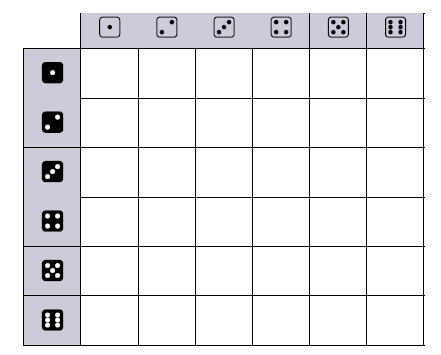
1. a. Reproduire et compléter le tableau à double entrée ci-dessous avec les sommes obtenues.
(Modéliser l'ensemble des issues par un tableau à double entrée )
Solution
1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
1 | 2 | 3 | 4 | 5 | 6 | 7 |
2 | 3 | 4 | 5 | 6 | 7 | 8 |
3 | 4 | 5 | 6 | 7 | 8 | 9 |
4 | 5 | 6 | 7 | 8 | 9 | 10 |
5 | 6 | 7 | 8 | 9 | 10 | 11 |
6 | 7 | 8 | 9 | 10 | 11 | 12 |
Question
b. Quel est la somme la plus fréquemment obtenue lors des tirages ?
Solution
La somme la plus fréquente lors des tirages est 7.
Question
c.Sachant que les deux dés sont équilibrés, complété le tableau ci-dessous :
S :Somme | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|
p(S) |
On appelle ce tableau la \(\color{magenta}{loi de probabilité}\) des sommes obtenues.
Solution
Loi de probabilité des sommes :
S :Somme | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|
p(S) | \(\frac{1}{36}\) | \(\frac{2}1{36}=\frac{1}{18}\) | \(\frac{3}{36}=\frac{1}{12}\) | \(\frac{4}{36}=\frac{1}{9}\) | \(\frac{5}{36}\) | \(\frac{6}{36}=\frac{1}{6}\) | \(\frac{5}{36}\) | \(\frac{4}{36}=\frac{1}{9}\) | \(\frac{3}{36}=\frac{1}{12}\) | \(\frac{2}{36}=\frac{1}{18}\) | \frac{1}{36} |
2. Déterminer les probabilités des événements suivants :
Question
a. Obtenir une somme égale à 4.
Solution
p(A)=p("obtenir une somme de 4")=\(\frac{3}{36}=\frac{1}{12}\)
Question
b. Obtenir une somme égale à 12.
Solution
\(p(B)p(\textbf{"obtenir une somme égale à 12"})=\frac{1}{36}\)
Il s"agit d'un événement élémentaire.
Question
c. Obtenir une somme supérieure ou égale à 7.
Solution
p(C)=p("obtenir une somme supérieure ou égale à 7")\(=\frac{21}{36}=\frac{7}{12}\)
Question
d. Obtenir une somme strictement inférieure à 4. e) Obtenir une somme paire. 3.
Solution
p(D)=p("obtenir une somme strictement inférieure à 4")=\(\frac{3}{36}=\frac{1}{12}\)
Question
3.Déterminer la probabilité de l'événement « Obtenir à la fois une somme égale à 7 et un produit égal à 12 ».
Solution
3.p( F)=p(« Obtenir à la fois une somme égale à 7 et un produit égal à 12 »)=\(\frac{2}{36}=\frac{1}{18}\)
car F={(3,4),(4,3)}
Question
4. On considère les deux événements définis par :
A : « Le résultat est pair »
B : « Le résultat est strictement supérieur à 7 »
Déterminer p(A), p(B).
Solution
\(p(A)=p( « Le résultat est pair »)=\frac{18}{36}=\frac{1}{2}\)
\(p(B)=p( « Le résultat est strictement supérieur à 7 »)=\frac{15}{36}=\frac{5}{12}\)
Question
5. Définir l'évènement \(\overline{B}\) par une phrase puis calculer sa probabilité.
Solution
\(\overline{B} : « Le résultat est inférieur ou égal à 7 »\)
\(p(\overline{B})=1-\frac{5}{12}=\frac{12}{12}-\frac{5}{12}=\frac{7}{12}\)
Question
6. Définir l'évènement A∪B par une phrase puis calculer sa probabilité.
Solution
\(A \cup B :\) « Le résultat est pair » ou « Le résultat est strictement supérieur à 7 »
\(p(A \cup B)=\frac{24}{36}=\frac{2}{3}\)
Question
7. Définir l'évènement A∩B par une phrase puis calculer sa probabilité
Solution
\(A \cap B :\) « Le résultat est pair » et « Le résultat est strictement supérieur à 7 »
\(p(A \cap B)=\frac{9}{36}=\frac{1}{4}\)
Question
8. Vérifier la formule
\(p(A \cup B)=p(A)+p(B)-p(A \cap B)\)
Solution
\(p(A \cup B)=\frac{2}{3}\)
\(p(A)=\frac{1}{2}\)
\(p(B)=\frac{5}{12}\)
\(p(A \cap B)=\frac{1}{4}\)
\(p(A)+p(B)-p(A \cap B)=\frac{1}{2}+\frac{5}{12}-\frac{1}{4}\)
\(\iff p(A)+p(B)-p(A \cap B)=\frac{6}{12}+\frac{5}{12}-\frac{3}{12}\)
\(\iff p(A)+p(B)-p(A \cap B)=\frac{8}{12}=\frac{2}{3}\)
donc \(p(A \cup B)=p(A)+p(B)-p(A \cap B)\)