Exercice : Dates anniversaires
On suppose que, pour chaque personne, tous les mois d'anniversaires sont équiprobables et on les notes de 1 à 12.
Question
Dans un groupe de quatre personnes prises au hasard, quelle est la probabilité que deux d'entre elles au moins fêtent leur anniversaire le même mois ?
Solution
On suppose que, pour chaque personne, tous les mois d'anniversaires sont équiprobables et on les notes de 1 à 12.
Calculons la probabilité de l'événement contraire, c'est à dire chaque élève a un mois d'anniversaire différent,
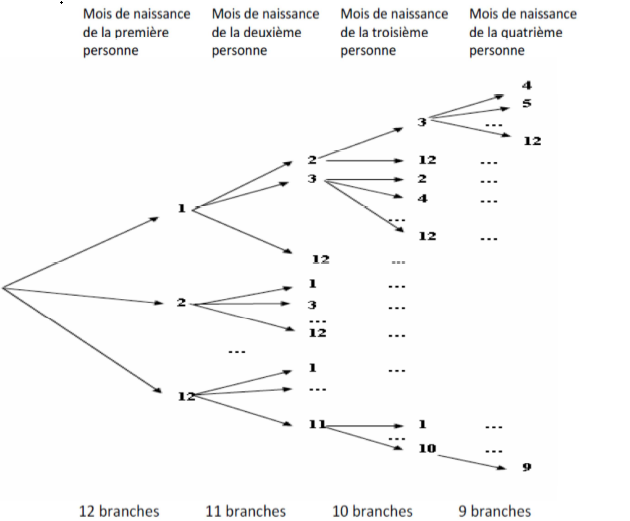
cela donne pour le premier élève : 12 choix
cela donne pour le second élève : 11 choix.
cela donne pour le troisième élève : 10 choix
cela donne pour le quatrième élève : 9 choix
\(p=\frac{12\times 11 \times 10 \times 9}{12^{4}}=\frac{11 880}{20 736}=\frac{55}{96}\simeq0,573\)
Soit une probabilité de environ 42,7% que 2 des 4 personnes soient nées le même mois
Question
1.On suppose que, pour chaque personne, tous les jours d'anniversaires sont équiprobables et on les notes de 1 à 31.
Dans une classe de 32 élèves quelle est la probabilité que deux d'entre elles au moins fêtent leur anniversaire le même jour ?
Solution
La probabilité de cet événement vaut 1 soit 100% car on ne peut pas ranger 32 dates d'anniversaires dans 31 dates sans utiliser au moins 2 fois une des deux dates.
Le principe est le même que pour vos chaussettes, essayer de ranger 3 paires de chaussettes dans deux tiroirs, il faudra en mettre en mettre deux dans un même tiroir.
Question
On suppose que, pour chaque personne, tous les jours d'anniversaires sont équiprobables et on les notes de 1 à 31.
Dans une classe de 31 élèves quelle est la probabilité que deux d'entre elles au moins fêtent leur anniversaire le même jour ?
Solution
Calculons la probabilité de l'événement contraire, c'est à dire chaque élève a un jour d'anniversaire différent,
cela donne pour le premier élève : 31 choix
cela donne pour le second élève : 30 choix
\(\dots\)
cela donne pour l'avant dernier élève : 2 choix
cela donne pour le dernier élève : 1 choix
\(p=\frac{31\times30\times \dots \times 1}{31^{31}}=4,8 \times 10^{-13}\simeq 0\)
Donc la probabilité que deux personnes soient nées le même jour est de 1 soit 100%