Exercice : Bancs
Un square est équipé de trois bancs à deux places séparés de 10 mètres l'un de l'autre.
Deux personnes arrivent successivement et s'installent au hasard.
Quelle est la probabilité que ces personnes soient assises côte à côte ?
\(\color{red}{\textbf{3. Expliquer la différence observée entre les deux probabilité obtenues : quelle en est la cause ?}}\)
Question
\(\color{red}{\textbf{1ère méthode : On considéré que les places sont numérotés de 1 a 6.}}\)
la première personne choisit un numéro, puis la deuxième en choisit un à son tour parmi les numéro restants. une issue possible de l'expérience est codée sous la forme d'un couple de nombres.
Le couple (2;5) par exemple signifie que la première personne a choisit le numéro 2 et la deuxième le numéro 5.
a. A l'aide d'un arbre présenté soigneusement , indiquer les issues possibles de cette expérience.
b. quelles sont les issues possibles pour lesquelles les deux personnes sont l'une à côté de l'autre en déduire la probabilité.
Solution
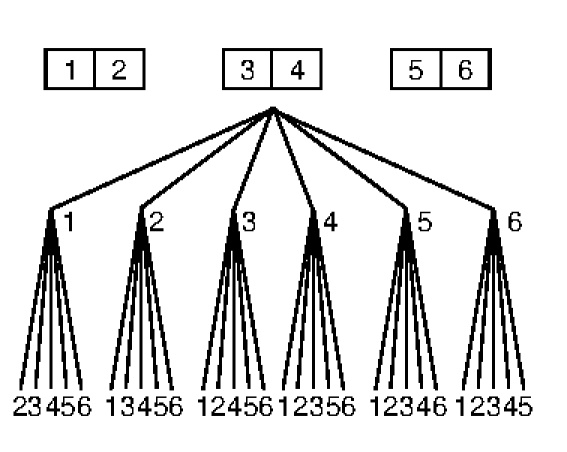
b) Les issues possibles sont (1,2) ,(1,3) ,(1,4),(1,5),(1,6),(2,1),(2,3),(2,4),(2,5),(2,6)....(6,5)
Il y a donc \(6\times 5 = 30\) issues possibles.
Celles qui correspondent à deux personnes assises côte à côte sont :
(1;2) ; (2;1) ; (3;4) ; (4;3) ; (5;6) et (6;5)
E l'événement "les personnes sont assises côte à côte"
$P(E) = \(\frac{6}{30} = \frac{1}{5}\)
Question
\(\color{red}{\textbf{2ème méthode : les bancs sont désignés par les lettres a, b, c}}\)
La première personne choisit un banc et la deuxième agit de même.
a. à l'aide d'un arbre présenté soigneusement , indiquer les issues possibles de cette expérience aléatoire.
b. calculer la probabilité que les deux personnes soient assises côte à côte.
Solution
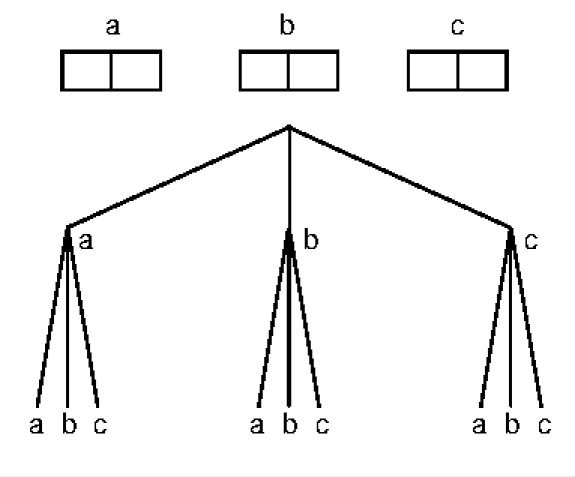
Les issues sont :
1ère personne s'assoit sur sur le banc | 2ème personne s'assoit sur sur le banc |
|---|---|
a | a |
a | b |
a | c |
b | a |
b | b |
b | c |
c | a |
c | b |
c | c |
" 2 personnes assises sur le même banc" correspond aux issues (a,a), (b,b) et (c,c) soit 3 issues sur 9
E' : l'événement " 2 personnes assises sur le même banc"
p(E')=\(\frac{3}{9}=\frac{1}{3}\)
Question
\(\color{red}{\textbf{3. Expliquer la différence observée entre les deux probabilité obtenues : quelle en est la cause ?}}\)
Solution
On voit que \(P(E) < P(E')\)
En pourcentages, on dirait qu'on a 20% de chances de réaliser l'événement E et environ 33% de réaliser l'événement E'
L'expérience aléatoire n'est pas suffisamment décrite au départ : il faut indiquer si l'on choisit la place (1er cas) ou le banc au hasard (2ème cas).
Ces deux descriptions conduisent à des résultats différents.
Et sans la procédure du choix au hasard, l'expérience aléatoire n'existe pas.