Exercice : Pion échiquié
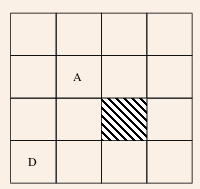
Un pion est posé sur la case marqué « D » du quadrillage ci-dessous.
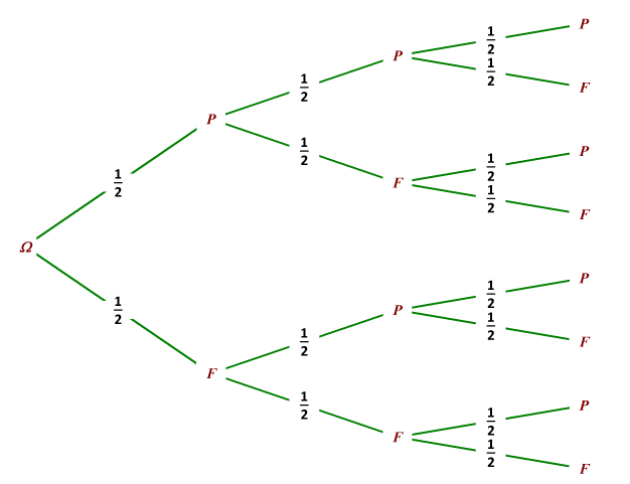
On lance trois fois de suite une pièce bien équilibrée. À chaque fois qu'on obtient « Pile », on déplace le pion d'une case vers la droite. Chaque fois qu'on obtient « Face » on le déplace d'une case vers le haut.
Ainsi, si par exemple on a obtenu deux « Piles » et un « Face », le pion se trouve finalement sur la case marquée « A ».
Question
Quelle est la probabilité qu'à l'issue des trois déplacements le pion se trouve sur la case hachurée?
Solution
Pour arriver à la case hachurée, il faut se déplacer deux fois à droite (deux piles ) et une fois vers le haut (une face). Chaque déplacement pouvant se faire dans n'importe quel ordre donc
A :"Arriver sur la case hachurée"
A={(P,P,F),(P,F,P),(F,P,P)} soit p(A)=\(\frac{3}{8}\)