Exercice : Roue colorée
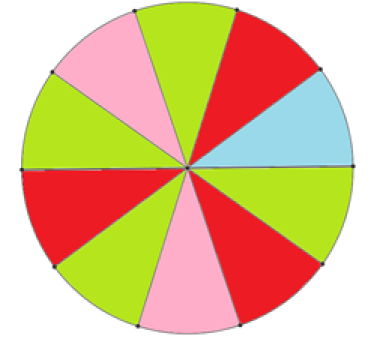
Une roue de loterie est partagée en dix secteurs de quatre couleurs différentes (bleu, rouge, vert et rose), comme représenté sur la figure ci-contre.
Quand on lance cette roue, elle tourne, puis s'arrête librement devant le repère.
On suppose que tous les secteurs ont la même probabilité de s'arrêter devant le repère.
Question
1. Calculer la probabilité d'obtenir chacune de quatre couleurs.
Solution
p("obtenir un secteur rouge")=\(\frac{3}{10}\)
p("obtenir un secteur vert")=\(\frac{4}{10}=\frac{2}{5}\)
p("obtenir un secteur bleu")=\(\frac{1}{10}\)
p("obtenir un secteur rose")=\(\frac{2}{10}=\frac{1}{5}\)
2. Pour jouer à cette loterie, on donne10 €, puis on tourne la roue.
• Si la couleur sortie est le bleu, on perçoit 40 €
• Si c'est le rose, on perçoit 25 €
• Si c'est le rouge, on perçoit 5 €
• Si c'est le vert, on ne perçoit rien.
Question
a. Détermine la probabilité du gain que l'on peut obtenir à cette loterie (suivant la couleur sortie).
Solution
p("perdre 5€")=\(\frac{3}{10}\)
p("perdre 10€")=\(\frac{4}{10}=\frac{2}{5}\)
p("gagner 30€")=\(\frac{1}{10}\)
p("gagner 15€")=\(\frac{2}{10}=\frac{1}{5}\)
Question
b. Marie affirme : « Si je joue une fois à la loterie, j'ai moins d'une chance sur trois de gagner de l'argent, alors je ne jouerai pas ». A-t-elle raison ? Justifier.
Solution
Probabilité de tomber sur un secteur me faisant gagner de l'argent :
p("gagner 30€")+p("gagner 15€")=\(\frac{1}{10}+\frac{2}{10}=\frac{3}{10}\)
donc Marie a raison d'affirmer qu'elle ai moins d'une chance sur trois de gagner de l'argent.
Par contre le gain possible est de :
Gain= p("perdre 5€") \times (-5) +p("perdre 10€") \times (-10)+p("gagner 30€")\times 30+ p("gagner 15€") \times 15
Gain=\(\frac{3}{10} \times (-5)+ \frac{4}{10} \times (-5)+\frac{1}{10} \times 30 +\frac{1}{5} \times 15\)
\(Gain=\frac{-15}{10} + \frac{-20}{10} +\frac{30}{10} +\frac{15}{5}\)
\(Gain=-1,5 -2+3 +3=2 ,5\)
donc en jouant à ce jeu, on gagne en moyenne 2,5 € donc sur un grand nombre de parties, on a intérêt à jouer.