Exercice : Canoé
Un groupe de quatre amis, Alphonse, Bernadette, Claude et Denis, décide de descendre l'Ill en canoé un dimanche après-midi.
Ils louent un canoé à deux places et deux canoés à une place.
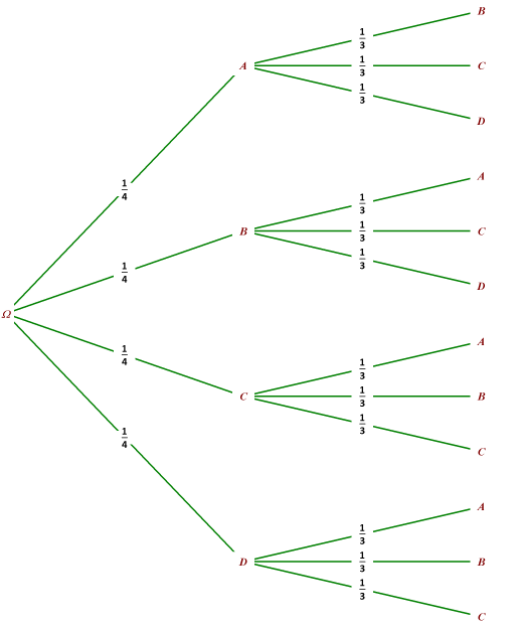
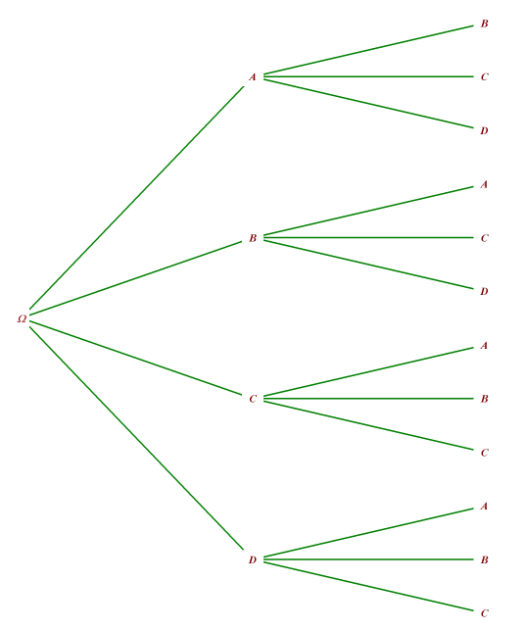
Ils se répartissent dans les trois embarcations en écrivant leurs noms sur des morceaux de papier puis tirent au hasard deux noms pour occuper le canoé à deux places.
Déterminer la probabilité de l'événement :
Exposer soigneusement la démarche mise en œuvre pour déterminer les résultats.
Question
1. "Alphonse est seul dans un canoé"
Question
2. "Bernadette et Claude sont ensemble dans le canoé à deux places"
Solution
.Les issues correspondantes sont (B,C),(C,B)
p("Bernadette et Claude sont ensemble dans le canoé à deux places")=\(2 \times \frac{1}{4} \times \frac{1}{3}=\frac{2}{12}=\frac{1}{6}\)
Question
3. " Claude et Denis sont chacun dans un canoé à une place."
Solution
p(" Claude et Denis sont chacun dans un canoé à une place.")=\(p(\overline{\textbf{"Bernadette et Claude sont ensemble dans le canoé à deux places"}})\)=\(1-\frac{1}{6}=\frac{5}{6}\)