Exercice : Tennis en double
Quatre amis Alice, Bob, Camille et Désiré se réunissent chaque semaine pour jouer une partie de tennis en double.
Ils ont décidé de former à chaque fois deux équipes au hasard.
Pour effectuer ce choix aléatoire, ils placent quatre cartons indiscernables au toucher marqués respectivement de leurs initiales A, B, C et D dans un sac.
L'un d'eux prélève un premier carton puis un second (sans remettre le premier).
Les deux amis dont les initiales figurent sur les deux cartons jouent la partie contre les deux autres.

Question
1. Quelle est la probabilité que le premier carton prélevé soit marqué B?
Solution
1 carton sur 4 porte l'indication B :
\(p("premier carton prélevé soit marqué B")=\frac{1}{4}\)
Question
2. La semaine dernière, Alice et Bob ont joué ensemble.Quelle est la probabilité qu'ils ne jouent pas à nouveau ensemble cette semaine?(On pourra s'aider d'un arbre pour répondre)
Solution
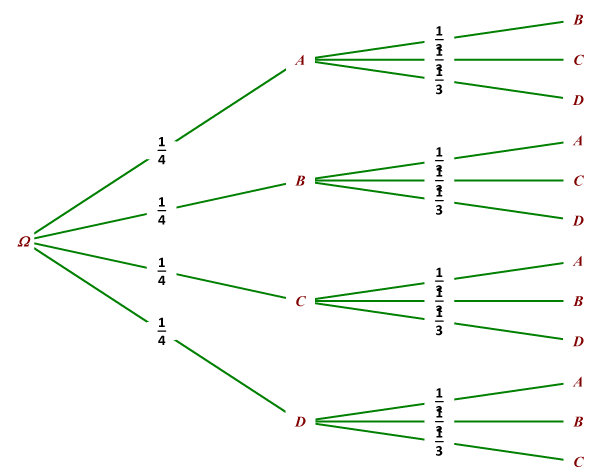
Alice et Bob joueront ensemble si
les cartons tirés sont (A ;B) ,(B ;A)
mais aussi (C ;D) et (D ;C)
donc
p("Alice et Bob jouent ensemble cette semaine"))
\(=\frac{1}{4} \times \frac{1}{3}+\frac{1}{4} \times \frac{1}{3}+\frac{1}{4} \times \frac{1}{3}+\frac{1}{4} \times \frac{1}{3}\)
\(=\frac{4}{12}\)
\(=\frac{1}{3}\)
p("Alice et Bob ne jouent pas ensemble cette semaine"))
=1-p("Alice et Bob jouent ensemble cette semaine"))
=\(1-\frac{1}{3}\)
=\(\frac{3}{3}-\frac{1}{3}\)
=\(\frac{2}{3}\)