Exercice : Résoudre 2
Question
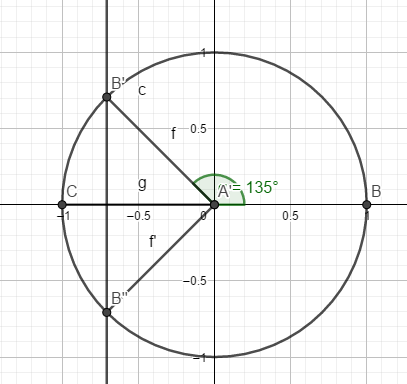
1. Déterminer l'ensemble de tous les nombres réels \(x\) tels que \(\cos\left(x\right)=-\frac{\sqrt{2}}{2}.\)
Solution
\(\cos\left(x\right)=-\frac{\sqrt{2}}{2}\)
\(\iff \begin{cases}x=\pi-\frac{\pi}{4}+2k\pi\\x=\pi+\frac{ \pi}{4}+2k\pi\end{cases}\) \(k \in\mathbb{Z}\)
\(\iff \begin{cases}x=\frac{4\pi}{4}-\frac{\pi}{4}+2k\pi\\x=\frac{4\pi}{4}+\frac{\pi}{4}+2k\pi\end{cases}\) \(k \in\mathbb{Z}\)
\(\iff \begin{cases}x=\frac{3\pi}{4}+2k\pi\\x=\frac{5\pi}{4}+2k\pi\end{cases}\) \(k \in\mathbb{Z}\)
Question
2. Donner, sous forme exacte, toutes les solutions qui appartiennent à l'intervalle \([-\pi;2\pi].\)
Solution
Pour \(k=0\)
\(\begin{cases}x=\frac{3\pi}{4}\\x=\frac{5\pi}{4}\end{cases}\)
Ces deux valeurs conviennent car elles appartiennent à l'intervalle \([-\pi;2\pi].\)
Pour \(k=1\)
\(\begin{cases}x=\frac{3\pi}{4}+2\pi\\x=\frac{5\pi}{4}+2\pi\end{cases}\)
Ces deux valeurs ne conviennent pas car elles sont supérieures à \(2\pi\)
Inutile de prendre des valeurs de k supérieures à 1 car les valeurs obtenues ne pourront pas appartenir à l'intervalle \([-\pi;2\pi].\)
Pour \(k=-1\)
\(\begin{cases}x=\frac{3\pi}{4}+2 \times (-1) \times \pi\\x=\frac{5\pi}{4}+2 \times (-1) \times \pi\end{cases}\)
\(\iff \begin{cases}x=\frac{3\pi}{4}-2\pi\\x=\frac{5\pi}{4}-2\pi\end{cases}\)
\(\iff \begin{cases}x=\frac{3\pi}{4}-\frac{8\pi}{4}\\x=\frac{5\pi}{4}-\frac{8\pi}{4}\end{cases}\)
\(\iff \begin{cases}x=\frac{-5\pi}{4}\\x=\frac{-3\pi}{4}\end{cases}\)
Seule la seconde valeur appartient à l'intervalle \([-\pi ;2\pi]=[-\frac{4\pi}{4} ;\frac{8\pi}{4}]\)
Pour \(k=-2\)
\(\begin{cases}x=\frac{3\pi}{4}+2 \times (-2) \times \pi\\x=\frac{5\pi}{4}+2 \times (-2) \times \pi\end{cases}\)
\(\iff \begin{cases}x=\frac{3\pi}{4}-4\pi\\x=\frac{5\pi}{4}-4\pi\end{cases}\)
\(\iff \begin{cases}x=\frac{3\pi}{4}-\frac{16\pi}{4}\\x=\frac{5\pi}{4}-\frac{16\pi}{4}\end{cases}\)
\(\iff \begin{cases}x=\frac{-13\pi}{4}\\x=\frac{-11\pi}{4}\end{cases}\)
Ces deux valeurs ne conviennent pas car elles sont inférieures à \(-\pi\)
Inutile de prendre des valeurs de k inférieures à -2 car les valeurs obtenues ne pourront pas appartenir à l'intervalle \([-\pi;2\pi]\)
Finalement :
\(\begin{cases}x=\frac{-3\pi}{4}\\\frac{3\pi}{4}\\x=\frac{5\pi}{4}\\\end{cases}\)