Exercice : Résoudre 4
Résoudre dans \(\mathbf{R}\) les équations trigonométriques suivantes,
puis donnez les mesures principales des angles correspondants.
Question
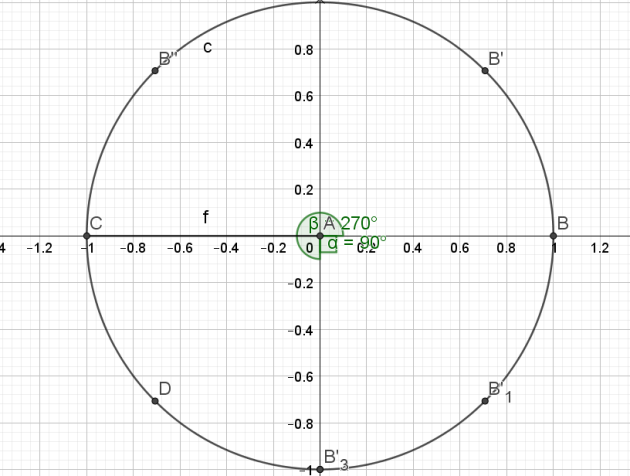
a. \(sin x = -\frac{1}{2}\)
Solution
\(\begin{cases}x=-\frac{\pi}{6}+2k\pi\\x=\pi - \frac{\pi}{6} +2 k\pi\end{cases}\) \(k\in \mathbb{Z}\)
\(\iff \begin{cases}x=-\frac{\pi}{6}+2k\pi\\x=\frac{6\pi}{6} - \frac{\pi}{6} +2 k\pi\end{cases}\) \(k\in \mathbb{Z}\)
\(\iff \begin{cases}x=-\frac{\pi}{6}+2k\pi\\x=\frac{5\pi}{6} +2 k\pi\end{cases}\) \(k\in \mathbb{Z}\)
\(\iff \begin{cases}x=-\frac{\pi}{6}+2k\pi\\x=\frac{5\pi}{6} +2 k\pi\end{cases}\) \(k\in \mathbb{Z}\)
Détermination des mesures principales :
Pour k=0
\(\begin{cases}x=-\frac{\pi}{6}\\x=\frac{5\pi}{6}\end{cases}\)
Ces deux mesures appartiennent à \(]-\pi ;\pi]\)
Pour k=1
\(\begin{cases}x=-\frac{\pi}{6}+2\pi\\x=\frac{5\pi}{6}+2\pi\end{cases}\)
\(\iff \begin{cases}x=-\frac{\pi}{6}+\frac{12\pi}{6}\\x=\frac{5\pi}{6}+\frac{12\pi}{6}\end{cases}\)
\(\iff \begin{cases}x=\frac{13\pi}{6}\\x=\frac{17\pi}{6}\end{cases}\)
Ces deux mesures n'appartiennent pas à \(]-\pi ;\pi]\)
Inutile de prendre des valeurs de k plus grandes.
Pour k=-1
\(\begin{cases}x=-\frac{\pi}{6}-2\pi\\x=\frac{5\pi}{6}-2\pi\end{cases}\)
\(\iff \begin{cases}x=-\frac{\pi}{6}-\frac{12\pi}{6}\\x=\frac{5\pi}{6}-\frac{12\pi}{6}\end{cases}\)
\(\iff \begin{cases}x=\frac{-11\pi}{6}\\x=\frac{-7\pi}{6}\end{cases}\)
Ces deux mesures n'appartiennent pas à \(]-\pi ;\pi]\)
Inutile de prendre des valeurs de k plus petites.
Les mesures principales sont donc
\(\begin{cases}x=-\frac{\pi}{6}\\x=\frac{5\pi}{6}\end{cases}\)
Question
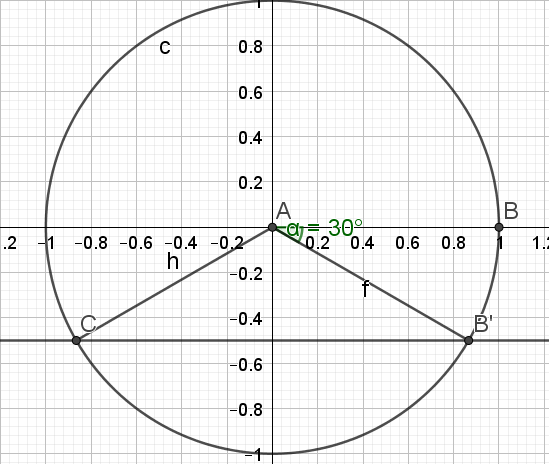
b. \(2 cos x = -2\)
Solution
\(2cos x = -2\)
\(\iff cos x = -1\)
\(\iff \begin{cases}x =\pi+2k\pi \\x=-\pi +2k\pi \end{cases}\) \(k\in \mathbb{Z}\)
Pour k=0
\(\begin{cases}x=\pi\\x=-\pi\end{cases}\)
Seule la première mesure appartient à \(]-\pi ;\pi]\)
Pour k=1
\(\begin{cases}x=\pi+2\pi\\x=-pi+2\pi\end{cases}\)
\(\iff \begin{cases}x=3\pi\\x=\pi\end{cases}\)
Seule la deuxième mesure appartient à \(]-\pi ;\pi]\)
mais on l'a déjà rencontrée pour k=0
Pour k=-1
\(\begin{cases}x=\pi-2\pi\\x=-\pi-2\pi\end{cases}\)
\(\iff \begin{cases}x=-\pi\\x=-3\pi\end{cases}\)
Ces deux mesures n'appartiennent pas à \(]-\pi ;\pi]\)
Inutile de prendre des valeurs de k plus petites.
Les mesures principales sont donc :
\(x=\pi\)
Question
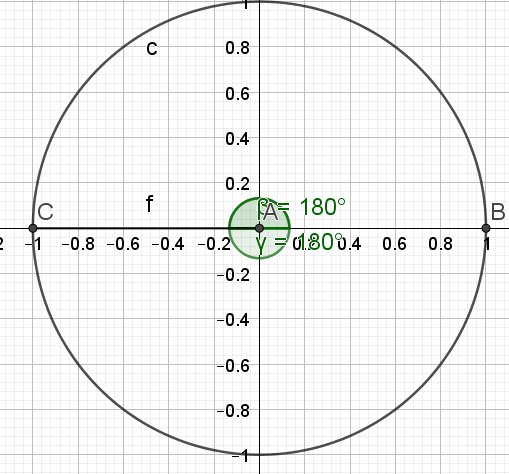
\(c. sin^2 x = 0\)
Solution
\(sin^2 x = 0\)
\(\iff sin x=0\)
\(\iff \begin{cases}x =0+2k\pi \\x=\pi +2k\pi \end{cases}\) \(k\in \mathbb{Z}\)
Pour k=0
\(\begin{cases}x=0\\x=\pi\end{cases}\)
Ces deux mesures appartient à \(]-\pi ;\pi]\)
Pour k=1
\(\begin{cases}x=0+2\pi\\x=\pi+2\pi\end{cases}\)
\(\iff \begin{cases}x=2\pi\\x=3\pi\end{cases}\)
Ces deux mesures appartient à \(]-\pi ;\pi]\)
Inutile de prendre des valeurs de k plus grandes.
Pour k=-1
\(\begin{cases}x=0-2\pi\\x=\pi-2\pi\end{cases}\)
\(\iff \begin{cases}x=-2\pi\\x=-\pi\end{cases}\)
Ces deux mesures n'appartiennent pas à \(]-\pi ;\pi]\)
Inutile de prendre des valeurs de k plus petites.
Les mesures principales sont donc :
\(x=\pi et x=0\)
Question
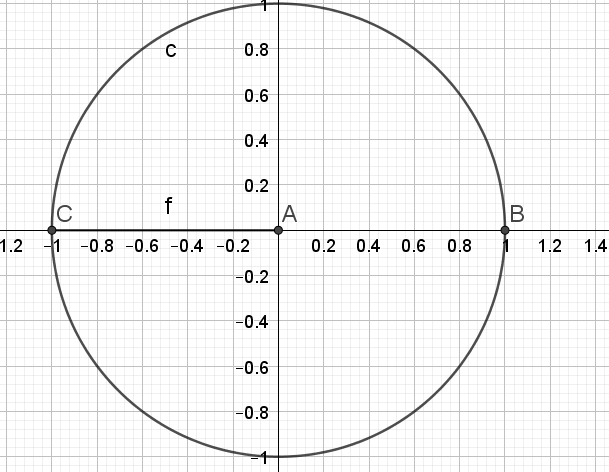
\(d. 2 sin^2 x - 1 = 0\)
Solution
\(2 sin^2 x - 1 = 0\)
\(\iff 2 sin^2 x = 1\)
\(\iff sin^2 x = \frac{1}{2}\)
\(\iff sin x = \sqrt{\frac{1}{2}}\) ou \(sin x = -\sqrt{\frac{1}{2}}\)
\(\iff sin x = \frac{1}{\sqrt{2}}\) ou \(sin x = -\frac{1}{\sqrt{2}}\)
\(\iff sin x = \frac{1\times \sqrt{2}}{\sqrt{2} \times \sqrt{2}}\) ou \(sin x = -\frac{1 \times \sqrt{2}}{\sqrt{2} \times \sqrt{2}}\)
\(\iff sin x = \frac{\sqrt{2}}{2}\) ou \(sin x = -\frac{\sqrt{2}}{2}\)
\(\iff \begin{cases}x = \frac{\pi}{4}+2k\pi\\x = \pi-\frac{\pi}{4}+2k\pi\end{cases}\)
ou \(\begin{cases}x = -\frac{\pi}{4}+2k\pi\\x = \pi-(-\frac{\pi}{4})+2k\pi\end{cases}\) \(k\in\mathbb{Z}\)
\(\iff \begin{cases}x = \frac{\pi}{4}+2k\pi\\x = \frac{4\pi}{4}-\frac{\pi}{4}+2k\pi\end{cases}\)
ou \(\begin{cases}x = -\frac{\pi}{4}+2k\pi\\x = \frac{4\pi}{4}-(-\frac{\pi}{4})+2k\pi\end{cases}\) \(k\in\mathbb{Z}\)
\(\iff \begin{cases}x = \frac{\pi}{4}+2k\pi\\x = \frac{3\pi}{4}+2k\pi\end{cases}\)
ou \(\begin{cases}x = -\frac{\pi}{4}+2k\pi\\x = \frac{4\pi}{4}+\frac{\pi}{4}+2k\pi\end{cases}\) \(k\in\mathbb{Z}\)
\(\iff \begin{cases}x = \frac{\pi}{4}+2k\pi\\x = \frac{3\pi}{4}+2k\pi\end{cases}\)
ou \(\begin{cases}x = -\frac{\pi}{4}+2k\pi\\x = \frac{5\pi}{4}+2k\pi\end{cases}\) \(k\in\mathbb{Z}\)
Pour k=0
\(\begin{cases}x = \frac{\pi}{4}\\x = \frac{3\pi}{4}\end{cases}\)
ou \(\begin{cases}x = -\frac{\pi}{4}\\x = \frac{5\pi}{4}\end{cases}\) \(k\in\mathbb{Z}\)
Seules les trois premières mesures appartiennent à \(]-\pi ;\pi]\)
Pour k=1
\(\begin{cases}x = \frac{\pi}{4}+2\pi\\x = \frac{3\pi}{4}+2\pi\end{cases}\)
ou \(\begin{cases}x = -\frac{\pi}{4}+2\pi\\x = \frac{5\pi}{4}+2\pi\end{cases}\)
\(\iff \begin{cases}x = \frac{\pi}{4}+\frac{8\pi}{4}\\x = \frac{3\pi}{4}+\frac{8\pi}{4}\end{cases}\)
ou \(\begin{cases}x = -\frac{\pi}{4}+\frac{8\pi}{4} \\x= \frac{5\pi}{4}+\frac{8\pi}{4}\end{cases}\)
\(\iff \begin{cases}x = \frac{9\pi}{4}\\x = \frac{11\pi}{4}\end{cases}\)
ou \(\begin{cases}x = \frac{7\pi}{4}\\ x= \frac{13\pi}{4}\end{cases}\)
Aucune des mesures n'appartient à \(]-\pi ;\pi]\)
Inutile de prendre des valeurs de k plus grandes.
Pour k=-1
\(\begin{cases}x = \frac{\pi}{4}-2\pi\\x = \frac{3\pi}{4}-2\pi\end{cases}\)
ou \(\begin{cases}x = -\frac{\pi}{4}-2\pi\\x = \frac{5\pi}{4}-2\pi\end{cases}\)
\(\iff \begin{cases}x = \frac{\pi}{4}-\frac{8\pi}{4}\\x = \frac{3\pi}{4}-\frac{8\pi}{4}\end{cases}\)
ou \(\begin{cases}x = -\frac{\pi}{4}-\frac{8\pi}{4} \\x= \frac{5\pi}{4}-\frac{8\pi}{4}\end{cases}\)
\(\iff \begin{cases}x = \frac{-7\pi}{4}\\x = \frac{-5\pi}{4}\end{cases}\)
ou \(\begin{cases}x = \frac{-9\pi}{4}\\ x= \frac{-3\pi}{4}\end{cases}\)
Seule la dernière valeur appartient à \(]-\pi ;\pi]\)
Inutile de prendre des valeurs de k plus petites pour les autres angles.
Pour k=-2
\(x = \frac{5\pi}{4}-2 \times 2\pi = \frac{5\pi}{4}-4\pi= \frac{5\pi}{4}-\frac{16\pi}{4}=\frac{-11\pi}{4}\notin ]-\pi ;pi]\)
Les mesures principales sont donc :
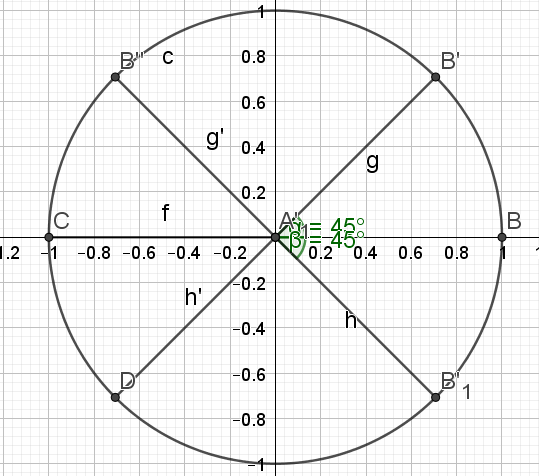
\(\begin{cases}x = \frac{\pi}{4}\\x = \frac{3\pi}{4}\\x = -\frac{\pi}{4}\\x = \frac{-3\pi}{4}\end{cases}\)
Question
e. \(2 sin x + 1 = 0\)
Solution
\(2 sin x + 1 = 0\)
\(\iff 2sin x = -1\)
\(\iff sin x = \frac{-1}{2}\)
\(\iff \begin{cases}x = -\frac{\pi}{2}+2k\pi\\x = \pi-(-\frac{\pi}{2})+2k\pi\end{cases}\) \(k\in\mathbb{Z}\)
\(\iff \begin{cases}x = -\frac{\pi}{2}+2k\pi\\x = \pi+\frac{\pi}{2}+2k\pi\end{cases}\) \(k\in\mathbb{Z}\)
\(\iff \begin{cases}x = -\frac{\pi}{2}+2k\pi\\x = \frac{2\pi}{2}+\frac{\pi}{2}+2k\pi\end{cases}\) \(k\in\mathbb{Z}\)
\(\iff \begin{cases}x = -\frac{\pi}{2}+2k\pi\\x = \frac{3\pi}{2}+2k\pi\end{cases}\) \(k\in\mathbb{Z}\)
Pour k=0
\(\begin{cases}x = -\frac{\pi}{2}\\x = \frac{3\pi}{2}\end{cases}\)
Les deux mesures appartiennent à \(]-\pi ;\pi]\)
Pour k=1
\(\begin{cases}x = -\frac{\pi}{2}+2\pi\\x = \frac{3\pi}{2}+2\pi\end{cases}\)
\(\iff \begin{cases}x = -\frac{\pi}{2}+\frac{4\pi}{2}\\x = \frac{3\pi}{2}+\frac{4\pi}{2}\end{cases}\)
\(\iff \begin{cases}x = \frac{3\pi}{2} \\x= \frac{7\pi}{2}\end{cases}\)
Seule la première valeur appartient à \(]-\pi ;\pi]\)
Inutile de prendre des valeurs de k plus grandes pour la première valeur.
Pour k=2
\(x = -\frac{\pi}{2}+2\times 2\pi\)
\(\iff x = -\frac{\pi}{2}+4\pi\)
\(\iff x = -\frac{\pi}{2}+\frac{8\pi}{2}\)
\(\iff x = \frac{7\pi}{2}\)
La valeur n'appartient pas à \(]-\pi ;\pi]\)
Inutile de prendre des valeurs de k plus grandes.
Pour k=-1
\(\begin{cases}x = -\frac{\pi}{2}-2\pi\\x = \frac{3\pi}{2}-2\pi\end{cases}\)\(es}\)
\(\iff \begin{cases}x = -\frac{\pi}{2}-\frac{4\pi}{2}\\x = \frac{3\pi}{2}-\frac{4\pi}{2}\end{cases}\)
ou \(\begin{cases}x = -\frac{5\pi}{2} \\x= -\frac{\pi}{2}\end{cases}\)
Seule la deuxième valeur appartient à \(]-\pi ;\pi]\)
Inutile de prendre des valeurs de k plus petites pour l'autre angle.
Pour k=-2
\(x = \frac{3\pi}{2}-2\times 2\pi\)
\(\iff x = \frac{3\pi}{2}-4\pi\)
\(\iff x = \frac{3\pi}{2}-\frac{8\pi}{2}\)
\(\iff x = \frac{-5\pi}{2}\)
La valeur n'appartient pas à \(]-\pi ;\pi]\)
Inutile de prendre des valeurs de k plus petites.
Les mesures principales sont donc :
\(\begin{cases}x = -\frac{\pi}{2}\\x = \frac{3\pi}{2}\end{cases}\)
Question
f. \(-sin^2 x = 1\)
Solution
\(-sin^2 x = 1\)
\(\iff sin^2 x = -1\)
or un carré est toujours positif donc \(S=\emptyset\)