Exercice : Résoudre 9
Résoudre les équations suivantes :
Question
1.\( \sin(3x)=0,5\)
Solution
\(sin(3x) =0,5=sin(\frac{\pi}{3}}\)
\(\begin{cases}3x=\frac{\pi}{3}+2k\pi\\3x=\pi-\frac{\pi}{3}+2k\pi\end{cases}\) \(k\in\mathbb{Z}\)
\(\iff \begin{cases}x=\frac{\pi}{9}+\frac{2k\pi}{3}\\3x=\frac{2\pi}{3}+2k\pi\end{cases}\)
\(\iff \begin{cases}x=\frac{\pi}{9}+\frac{2k\pi}{3}\\x=\frac{2\pi}{9}+\frac{2k\pi}{3}\end{cases}\)
\(k\in\mathbb{Z}\)
\(\iff \begin{cases}x=\frac{\pi}{9}+\frac{2k\pi}{3}\\x=\frac{2\pi}{9}+\frac{2k\pi}{3}\end{cases}\) \(k\in\mathbb{Z}\)
Les solutions dans \(\mathbb{R}\) sont donc :
\(\iff \begin{cases}x=\frac{\pi}{9}+\frac{2k\pi}{3}\\x=\frac{2\pi}{9}+\frac{2k\pi}{3}\end{cases}\) \(k\in\mathbb{Z}\)
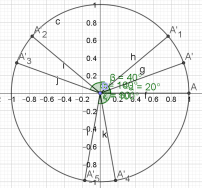
Recherche des solutions dans \(]-\pi ;\pi]\):
Pour k=0:
\(\begin{cases}x=\frac{\pi}{9}\\x=\frac{2\pi}{9}\end{cases}\)
Ces deux valeurs appartiennent à \(]-\pi ;pi]\)
Pour k=1 :
\(\begin{cases}x=\frac{\pi}{9}+\frac{2\pi}{3}\\x=\frac{2\pi}{9}+\frac{2\pi}{3}\end{cases}\) \(k\in\mathbb{Z}\)
\(\iff \begin{cases}x=\frac{\pi}{9}+\frac{6\pi}{9}\\x=\frac{2\pi}{9}+\frac{6\pi}{9}\end{cases}\)
\(\iff \begin{cases}x=\frac{7\pi}{9}\\x=\frac{8\pi}{9}\end{cases}\)
Ces deux valeurs appartiennent à \(]-\pi ;pi]\)
Pour k=2 :
\(\begin{cases}x=\frac{\pi}{9}+\frac{4\pi}{3}\\x=\frac{2\pi}{9}+\frac{4\pi}{3}\end{cases}\) \(k\in\mathbb{Z}\)
\(\iff \begin{cases}x=\frac{\pi}{9}+\frac{12\pi}{9}\\x=\frac{2\pi}{9}+\frac{12\pi}{9}\end{cases}\)
\(\iff \begin{cases}x=\frac{13\pi}{9}\\x=\frac{14\pi}{9}\end{cases}\)
Ces deux valeurs n'appartiennent à \(]-\pi ;pi]\)
Inutile de prendre des valeurs de \(k\) supérieures.
Pour k=-1 :
\(\begin{cases}x=\frac{\pi}{9}-\frac{2\pi}{3}\\x=\frac{2\pi}{9}-\frac{2\pi}{3}\end{cases}\) \(k\in\mathbb{Z}\)
\(\iff \begin{cases}x=\frac{\pi}{9}-\frac{6\pi}{9}\\x=\frac{2\pi}{9}-\frac{6\pi}{9}\end{cases}\)
\(\iff \begin{cases}x=\frac{-5\pi}{9}\\x=\frac{-4\pi}{9}\end{cases}\)
Ces deux valeurs appartiennent à \(]-\pi ;pi]\)
Pour k=-2 :
\(\begin{cases}x=\frac{\pi}{9}-\frac{4\pi}{3}\\x=\frac{2\pi}{9}-\frac{4\pi}{3}\end{cases}\) \(k\in\mathbb{Z}\)
\(\iff \begin{cases}x=\frac{\pi}{9}-\frac{12\pi}{9}\\x=\frac{2\pi}{9}-\frac{12\pi}{9}\end{cases}\)
\(\iff \begin{cases}x=\frac{-11\pi}{9}\\x=\frac{-10\pi}{9}\end{cases}\)
Ces deux valeurs n'appartiennent pas à \(]-\pi ;pi]\)
Inutile de prendre des valeurs de \(k\) inférieures.
Question
2. \(2\cos^{2}x-3cosx-2=0\). On pourra commencer par faire un changement de variable...
Solution
\(2\cos^{2}x-3cosx-2=0\).
\(X=cos x\)
\(\iff 2X^2 -3X -2 = 0\)
\(\Delta=b^2-4\times a \times c\)
\(\iff \Delta=(-3)^2-4\times 2 \times (-2)\)
\(\iff \Delta=9+16=25\)
\(\begin{cases}X_1=\frac{-b-\sqrt{\Delta}}{2a}\\X_2=\frac{-b+\sqrt{\Delta}}{2a}\end{cases}\)
\(\iff \begin{cases}X_1=\frac{-(-3)-\sqrt{25}}{2 \times 2}\\X_2=\frac{-(-3)+\sqrt{25}}{2 \times 2}\end{cases}\)
\(\iff \begin{cases}X_1=\frac{3-5}{4}\\X_2=\frac{3+5}{4}\end{cases}\)
\(\iff \begin{cases}X_1=\frac{-2}{4}\\X_2=\frac{8}{4}\end{cases}\)
\(\iff \begin{cases}X_1=\frac{-1}{2}\\X_2=2\end{cases}\)
L'équation \(cos x_2=2\) n'admet pas de solution car \(cos x\in[-1 ;1]\)
\(cos x_1=\frac{-1}{2}\)
\(\iff cos x_1=cos (\frac{2\pi}{3})\)
\(\begin{cases} x_1=\frac{2\pi}{3}+2k\pi\\x_1=\frac{-2\pi}{3}+2k\pi\end{cases}\)
Les solutions sur \(\mathh{R}\) sont :
\(\begin{cases} x_1=\frac{2\pi}{3}+2k\pi\\x_1=\frac{-2\pi}{3}+2k\pi\end{cases}\)
Les solutions sur \(]-\pi ;\pi]\) sont :
\(\begin{cases} x_1=\frac{2\pi}{3}\\x_2=\frac{-2\pi}{3}\end{cases}\)