Exercice : Résoudre 3
On se propose de résoudre l'équation \(\sin\left(3x\right)=\cos\left(x\right)\).
(De telles équations se présentent couramment dans l'étude de problèmes physiques, par exemple en mécanique ou en électronique)
Question
1. On considère un nombre réel quelconque \(x\).
Que peut-on dire des nombres réels \(\cos\left(x\right)\) et \(\sin\left(\dfrac{\pi}{2}-x\right)\)?
Solution
\(\sin\left(\dfrac{\pi}{2}-x\right)=\cos\left(x\right)\)
Question
2. En déduire que l'équation équivaut à: \(3x=\frac{\pi}{2}-x+2k\pi\) ou \(3x=\frac{\pi}{2}+x+2k\pi\),\(k\) désignant un nombre entier relatif quelconque.
Solution
\(\sin\left(3x\right)=\cos\left(x\right)=\sin\left(\dfrac{\pi}{2}-x\right)\)
\(\iff \sin\left(3x\right)=\cos\left(x\right)=\sin\left(\dfrac{\pi}{2}-x\right)\)
\(\iff \begin{cases}3x=\dfrac{\pi}{2}-x+2k\pi\\3x=\pi-(\dfrac{\pi}{2}-x)+2k\pi\end{cases}\) \(k \in \mathbb{Z}\)
\(\iff \begin{cases}3x=\dfrac{\pi}{2}-x+2k\pi\\3x=\pi-\dfrac{\pi}{2}+x+2k\pi\end{cases}\) \(k \in \mathbb{Z}\)
\(\iff \begin{cases}3x=\dfrac{\pi}{2}-x+2k\pi\\3x=\dfrac{\pi}{2}+x+2k\pi\end{cases}\) \(k \in \mathbb{Z}\)
Question
3. Déterminer les nombres réels \(x\) solutions de l'équation.
Solution
\(\begin{cases}3x=\dfrac{\pi}{2}-x+2k\pi\\3x=\dfrac{\pi}{2}+x+2k\pi\end{cases}\) \(k \in \mathbb{Z}\)
\(\iff \begin{cases}3x+x=\dfrac{\pi}{2}+2k\pi\\3x-x=\dfrac{\pi}{2}+2k\pi\end{cases}\) \(k \in \mathbb{Z}\)
\(\iff \begin{cases}4x=\dfrac{\pi}{2}+2k\pi\\2x=\dfrac{\pi}{2}+2k\pi\end{cases}\) \(k \in \mathbb{Z}\)
\(\iff \begin{cases}x=\dfrac{\pi}{8}+\frac{2k\pi}{4}\\x=\dfrac{\pi}{4}+k\pi\end{cases}\) \(k \in \mathbb{Z}\)
\(\iff \begin{cases}x=\dfrac{\pi}{8}+\frac{k\pi}{2}\\x=\dfrac{\pi}{4}+k\pi\end{cases}\) \(k \in \mathbb{Z}\)
Question
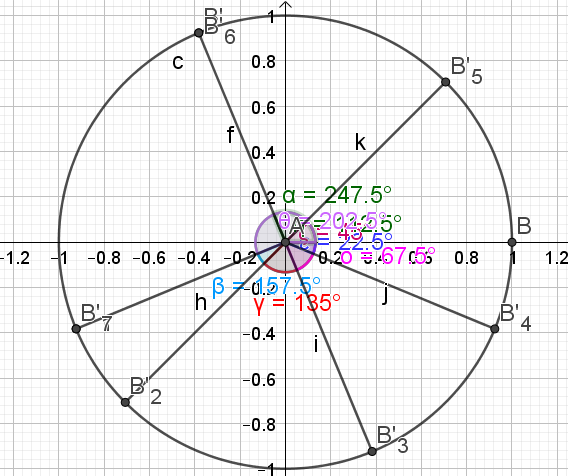
4. Placer sur le cercle trigonométrique les points correspondant aux solutions de l'équation.
Solution
Pour k=0 :
\(\begin{cases}x=\dfrac{\pi}{8}\\x=\dfrac{\pi}{4}\end{cases}\)
Pour k=1 :
\(\begin{cases}x=\dfrac{\pi}{8}+\frac{\pi}{2}\\x=\dfrac{\pi}{4}+\pi\end{cases}\)
\(\iff \begin{cases}x=\dfrac{\pi}{8}+\frac{4\pi}{8}\\x=\dfrac{\pi}{4}+\dfrac{4\pi}{4}\end{cases}\)
\(\iff \begin{cases}x=\dfrac{5\pi}{8}\\x=\dfrac{5\pi}{4}\end{cases}\)
Pour k=2 :
\(\begin{cases}x=\dfrac{\pi}{8}+\frac{2\pi}{2}\\x=\dfrac{\pi}{4}+2\pi\end{cases}\)
\(\begin{cases}x=\dfrac{\pi}{8}+\frac{8\pi}{8}\\x=\dfrac{\pi}{4}+2\pi=\dfrac{\pi}{4}\end{cases}\)
\(\iff \begin{cases}x=\dfrac{9\pi}{8}\\x=\dfrac{\pi}{4}+2\pi=\dfrac{\pi}{4}\end{cases}\)
Inutile d'aller plus loin pour le deuxième angle car on a retrouvé la valeur de l'angle pour k=0
Pour k=3 :
Pour le premier angle :
\(x=\dfrac{\pi}{8}+\frac{3\pi}{2}\)
\(\iff x=\dfrac{\pi}{8}+\frac{12\pi}{8}\)
\(\iff x=\dfrac{13\pi}{8}\)
Pour k=4 :
Pour le premier angle :
\(x=\dfrac{\pi}{8}+\frac{4\pi}{2}\)
\(\iff x=\dfrac{\pi}{8}+2\pi\)
\(\iff x=\dfrac{\pi}{8}\)
Inutile d'aller plus loin pour le premier angle car on a retrouvé la valeur de l'angle pour k=0
Pour k=-1 :
\(\begin{cases}x=\dfrac{\pi}{8}+\frac{-\pi}{2}\\x=\dfrac{\pi}{4}-\pi\end{cases}\)
\(\iff \begin{cases}x=\dfrac{\pi}{8}-\frac{4\pi}{8}\\x=\dfrac{\pi}{4}-\dfrac{4\pi}{4}\end{cases}\)
\(\iff \begin{cases}x=\dfrac{-3\pi}{8}\\x=\dfrac{-3\pi}{4}\end{cases}\)
Pour k=-2 :
\(\begin{cases}x=\dfrac{\pi}{8}+\frac{-2\pi}{2}\\x=\dfrac{\pi}{4}-2\pi\end{cases}\)
\(\iff \begin{cases}x=\dfrac{\pi}{8}-\frac{8\pi}{8}\\x=\dfrac{\pi}{4}\end{cases}\)
Inutile d'aller plus loin pour le premier angle car on a retrouvé la valeur de l'angle pour k=0
Pour k=-3 :
\(x=\dfrac{\pi}{8}+\frac{-3\pi}{2}\)
\(\iff x=\dfrac{\pi}{8}+\frac{-12\pi}{8}\)
\(\iff x=\dfrac{-11\pi}{8}\)
Pour k=-4 :
\(x=\dfrac{\pi}{8}+\frac{-4\pi}{2}\)
\(\iff x=\dfrac{\pi}{8}-2\pi\)
\(\iff x=\dfrac{\pi}{8}\)
Inutile d'aller plus loin pour le premier angle car on a retrouvé la valeur de l'angle pour k=0
\(\begin{cases} x=\dfrac{-11\pi}{8}\\x=\dfrac{-7\pi}{8}\\x=\dfrac{-3\pi}{4}\\x=\dfrac{-3\pi}{8}\\x=\dfrac{\pi}{8}\\x=\dfrac{\pi}{4}\\x=\dfrac{5\pi}{8}\\x=\dfrac{5\pi}{4}\\x=\dfrac{9\pi}{8}\\x=\dfrac{13\pi}{8}\end{cases}\)
\(\dfrac{9\pi}{8}=\dfrac{-7\pi}{8}\) car \(\dfrac{9\pi}{8}-\dfrac{-7\pi}{8}=\dfrac{16\pi}{8}=2\pi\)
\(\dfrac{-3\pi}{4}=\dfrac{5\pi}{4}\) \(\dfrac{5\pi}{4}-\dfrac{-3\pi}{4}=\dfrac{8\pi}{4}=2\pi\)
\(\dfrac{-3\pi}{8}=\dfrac{13\pi}{8}\) \(\dfrac{13\pi}{8}-\dfrac{-13\pi}{8}=\dfrac{16\pi}{8}=2\pi\)
Finalement les solutions sont :
\(\begin{cases}x=\dfrac{-11\pi}{8\\}x=\dfrac{\pi}{8}\\x=\dfrac{\pi}{4}\\x=\dfrac{5\pi}{8}\\x=\dfrac{5\pi}{4}\\x=\dfrac{9\pi}{8}\\x=\dfrac{13\pi}{8}\end{cases}\)